Von Pippi Langstrumpf lernen!

Wer kennt den Text nicht: «2 x 3 macht 4 -widdewiddewitt und 3 macht 9e!». Während zu Schulzeiten uns die Lehrer für dermassen schlechtes Rechnen zu allerlei Pirouetten verdonnerten, müsste heutzutage der Liedtext unter dem Kontext der Unsicherheit ganz anders interpretiert werden.

In einigen Blogbeiträgen haben wir die Box von Pandora, namentlich das Mantra, dass unter Unsicherheit 1 + 1 nicht gleich 2 gilt, bereits seziert (siehe Fluch der Mittelwerte, die Ausführungen zum cash-flow-at-risk, etc.). Auch bei der Multiplikation von Unsicherheiten werden die gängigen Rechneregeln auf den Kopf gestellt.

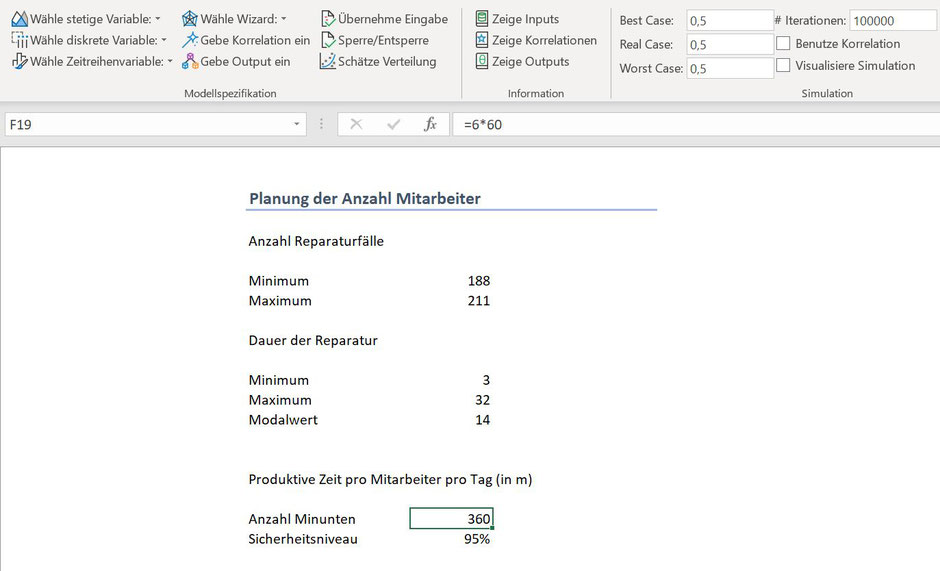
Es reicht auch hier auf ein ganz einfaches Beispiel einzugehen. Stellen wir uns vor, dass wir die Anzahl der Mitarbeiter aus dem Reparaturbetrieb einem Audit unterziehen müssen, um Kosten einzusparen. Zurzeit sind 16 Vollzeitmitarbeiter dort beschäftigt, wovon 2 Mitarbeiter Fluktuationen aufgrund von Ferienabwesenheiten. Krankheitsfälle etc. auffangen. Die Anzahl der Basismitarbeiter beträgt somit 14. Für jeden Vollzeitmitarbeiter sind 6 produktive Stunden pro Tag anzusetzen. In Spitzenzeiten werden zusätzlich externe, temporäre Arbeiter eingesetzt.

Aus der Vergangenheit wissen wir, dass pro Tag zwischen 188 und 211 Reparaturfälle behandelt werden und die Anzahl dieser Fälle gleichverteilt ist. Die Dauer einer Reparatur pro Fall kann ebenfalls anhand von Daten aus der Vergangenheit abgeleitet werden, diese entspricht einer PERT Verteilung (mit Minimum von 2 Minuten, einem Maximum von 32 Minuten und einem Modalwert von 14 Minuten).

Wie hoch ist die optimale Anzahl der Basismitarbeiter, wenn davon auszugehen ist, dass mit einer Sicherheit von 95% alle eingehenden Reparaturen am gleichen Tag erledigt werden können?

Die meisten Menschen würden die Grösse «Anzahl Reparaturen» und «Dauer Reparatur» nehmen und diese multiplizieren, um das gesuchte Ergebnis unter Einschluss der Sicherheit von 95% zu erhalten – und, ja, bätsch. Bevor wir dies genau analysieren: anbei das Resultat der «falschen» Berechnung, gefolgt von der «wahren» Berechnungsmethode, jeweils mit 100'000 Iterationen simuliert.

Während mit dem ersten Ansatz die Anzahl der Basismitarbeiter zwischen 2 und 19 Mitarbeiter schwankt (das 95% Konfidenzniveau – oder auch Sicherheit – liegt bei 14 Mitarbeiter), beträgt mit dem «wahren» Ansatz die Bandbreite nur zwischen 8 und 10 Mitarbeiter (das 95% Konfidenzniveau liegt in diesem Fall bei 9 Mitarbeiter).

Was ist schiefgelaufen? Bei der «falschen» Berechnung wird davon ausgegangen, dass die «Dauer Reparatur» für alle Reparaturfälle eines Tages gleich ist. Hier die Erklärung anhand eines Beispiels. Stellen wir uns vor, dass die Simulation in der i-ten Iteration eine Reparaturdauer von 4 Minuten ermittelt, gleichzeitig wird in dieser i-Iteration von 191 Reparaturfällen ausgegangen. Die Zeitdauer für alle Reparaturen beträgt demnach 4 Minuten/pro Reparaturfall * 191 Reparaturfälle = 764 Minuten, was einem Bedarf von 3 Mitarbeitern entspricht. Es ist jedoch unwahrscheinlich, schlicht fasst unmöglich, dass für alle aufeinanderfolgenden 191 Reparaturfälle jede Reparatur genau 4 Minuten dauert.

Korrekt ist, dass ausgehend von der Anzahl der Reparaturfälle die entsprechende Dauer pro Reparaturfall separat errechnet werden muss und die Summe dessen die Anzahl der Minuten der i-ten Iteration ergibt. Das fiktive Beispiel hierzu: die Anzahl Reparaturfälle beträgt 191; die Dauer der ersten Reparatur beträgt 20 Minuten, die der zweiten Reparatur 4 Minuten, usw. Die notwendige Bearbeitungszeit beträgt also 20 + 4 +….+. Aus dieser Konstellation ergibt sich die in obiger Darstellung ersichtliche Normal-ähnliche Verteilung.

Mit der korrekten Berechnungsmethode unter Einschluss der Simulation wird aufgezeigt, dass ein Grundstock von 9 Vollzeitmitarbeiter notwendig ist, 5 weniger als bisher als richtig angenommen.

Bei vielen Entscheidungsträgern wird der hier vorgestellte Sachverhalt Unmut erzeugen und sie in der Ansicht bestärken, dass das Rechnen unter Unsicherheit Teufelszeug darstellt. Wir entgegnen: Selbst die heute bekannte Mathematik wurde nicht über Nacht in die Köpfe der Menschen geimpft. Hier braucht es wiederholt Aufklärung und Erfahrung. Auch wir verstehen nicht alles. Das Schöne an den Simulationen aber ist, dass der Mensch nicht mehr rechnen muss. Er simuliert. Das ist die Zukunft.

P.S.: Bei all den Optimierungen, welche mit Simulationen möglich sind, dürfen wir eins nicht vergessen: die Entscheidung trifft der Mensch. Falls der Audit Konsequenzen für die Mitarbeiter haben sollte, dann sorgen Sie dafür, dass es positive sind.