- Deutsch
- Español
- English
- Blog
- Get it now!
- Shop
- Wiki
- DEU - Stetige Verteilungen
- Gleichverteilung
- Dreiecksverteilung
- Normalverteilung
- LogNormalverteilung
- Betaverteilung
- Gumbelverteilung
- Gammaverteilung
- Exponentialverteilung
- Gekürzte Normalverteilung
- Weibullverteilung
- Pareto-Verteilung
- Cauchy-Verteilung
- ArcSin-Verteilung
- F-Verteilung
- Student-t-Verteilung
- chi2-Verteilung
- PERT-Verteilung
- Fréchet-Verteilung
- Logistische Verteilung
- DEU - Diskrete Verteilungen
- DEU - Zeitreihen
- DEU - Weitere Funktionen
- Referenz
- Umgang mit Variablen
- Interpretation
- Benutzerdefinierte Verteilung
- Begrenzte Verteilungen
- Korrelationen
- Memory Calculation
- Output
- Multiple Simulation / Box-Whisker
- Bayes-Faktor
- Forecast-Tool
- Batch-Funktion
- Datenanpassung
- Benford Analyse
- Dos and don'ts
- Bootstrap
- Decision Information Package
- Spider Diagramm
- Naive Bayes Klassifikation
- Risikomatrix
- DEU - Stetige Verteilungen
MC FLO leicht gemacht - Beispiele
Hier sehen Sie an den mit MC FLO mitgelieferten Beispielen das breite Einsatzspektrum von MC FLO. Weitere Beispiele und die entsprechenden Excels finden Sie in unserem Blog.
Bayessche Statistik - Lernen AUS DATEN

Bayes_A_B_Test : Prüft eine Gruppe (Variation) gegenüber einer Kontrollgruppe auf Unterschiede.
Als Beispiel wird ein Test untersucht, bei der Probanden eine neue Homepage und eine alte Homepage vorfinden. Anhand der Anzahl Verkäufe soll herausgefunden werden, ob die neue Homepage (Variation) besser bei der Kundschaft ankommt oder nicht.
Mit einem Bayesschen A/B Test kommt die untersuchende Person zur Überzeugung, dass die Variation besser ist. Eine vollständige Überzeugung liegt anhand der gemessenen Daten jedoch nicht vor.

Bayes_Cyber_Attacks: Stellt anhand des Vorwissens und gemessenen Daten zu Cyberattacken eine Aussage zu zukünftigen Cyberattacken.
Das Vorwissen wird - bei Fehlen von Daten - anhand von (subjektiven) Einschätzungen und einer zugehörigen Wahrscheinlichkeitsverteilung beschrieben. Sobald Daten vorliegen, kann dieses mit dem Vorwissen anhand des Satzes von Bayes zu einer Posteriorverteilung überführt werden, Die Posteriorverteilung gibt Auskunft über die zukünftigen unsicheren Cyberattacken innerhalb einer Zeitspanne wieder.
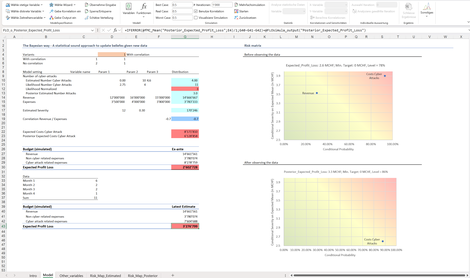
Bayes_CyberAttacks_1: Erweitert das in Cyber_Attacks beschriebene Problem um Zielvorgaben. Dabei werden die Auswirkungen der Einflussgrössen auf die Zielerreichung mit einer Risiko-Matrix dargestellt. Hierbei werden zwei disjunkte Szenarien anhand der Mehrfachsimulation analysiert
Das erste Szenario ignoriert mögliche Zusammenhänge (Korrelationen) zwischen den Einflussgrössen. Beim zweiten wird ein Zusammenhang einer Fréchet Copula berücksichtigt.
Sowohl vor als nach Beobachtung von Daten kann der Einfluss der Treibervariablen auf das Ergebnis anhand einer Risiko-Matrix dargestellt werden. Während vor Beobachtung die Cyber-Attacken als wesentlicher Treiber des Ergebnis klassifiziert werden können, kann nach Beobachtung eine Entwarnung ausgesprochen werden.
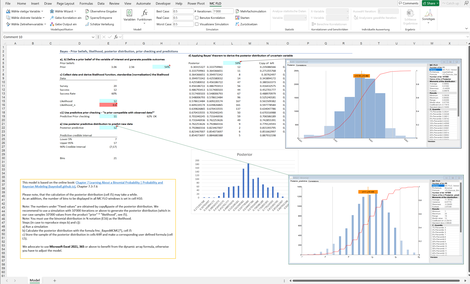
Bayes_I: Zeigt anhand der Bayessschen Statistik auf, wie "Lernen aus Daten" algorithmisch umgesetzt wird.
Ausgangspunkt ist ein Vorwissen - hier über die Zustimmung von Personen zu einer beliebigen Fragestellung. Annahme ist, dass 54% der Personen zustimmen. Die Zustimmungsrate gilt aber als unsicher. Diese kann zwischen ca. 17% und 87% variieren.
Bei einer Umfrage von 20 Teilnehmern befürworten 12 das Vorhaben. Das Umfrageergebnis kann als Resultat einer Binomialveteilung aufgefasst werden.
Durch Kombination von Vorwissen und Umfrageresultat kann das Wissen über die echte Zustimmungsquote geschärft und dessen Unsicherheit reduziert werden.
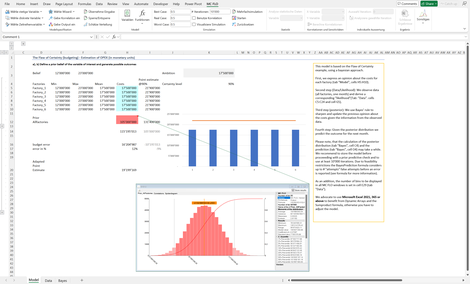
Bayes_II: Zeigt anhand der Fabrikplanung auf, wie der Bayessche Ansatz beim Zusammenspiel zwischen Prognose und Planung funktioniert.
Ausgangslage sind unsichere Grössen, wie mögliche Fabrikkosten pro Jahr. Diese werden anhand einer Gleichverteilung mittels Monte-Carlo Simulation aggregiert. Die Aggregation stellt den Prognoseraum dar. Aus diesem wird ein Zielwert abgeleitet.
Nach Messung von konkreten Kosten der Fabriken kann die Prognose geschärft, mit den Zielwerten gegenübergestellt und mögliche Handlungsempfehlungen abgeleitet werden.
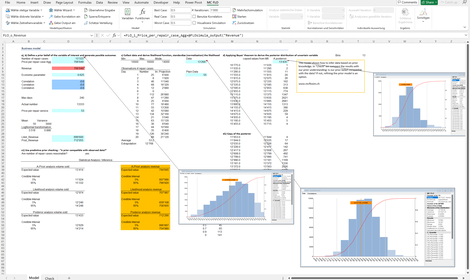
Bayes_III: Erneutes Beispiel zur Illustration von "Lernen aus Daten". Unsicheres Vorwissen wird mit gemessenen Daten anhand des Satzes von Bayes in ein angepasstes Wissen (Posterior) überführt. Dies als Wahrscheinlichkeitsverteilung vorliegende angepasste Wissen wird als Prognoseinstrument eingesetzt.
Unabhängig davon, kann das Verständnis des unsicheren Vorwissens - etwa abgeleitet aus Treibermodellen - mit den Daten verprobt werden. Liegen die Daten ausserhalb der Bandbreite des Vorwissens, entsteht kein Lerneffekt. Das Vorwissen kann nicht von den Daten profitieren. Umgekehrt bedeutet es, dass das Vorwissen nicht mit den Daten kompatibel ist. Es läge dann eine Missspezifikation vor. In diesem Beispiel sind die Daten mit dem Vorwissen kompatible und der Lerneffekt tritt ein.
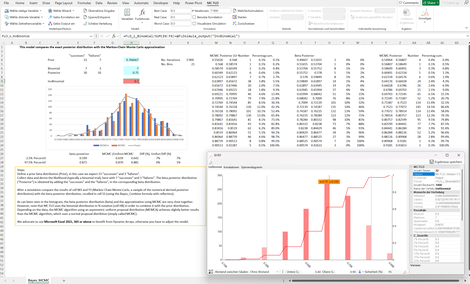
Bayes_Simple_Beta: Die Kombination von Vorwissen und gemessenen Daten zum "Posteriorwissen" anhand des Theorems von Bayes kann nur bei einfachen Wahrscheinlichkeitsverteilungen analytisch gelöst werden. Für alle anderen Verteilungen und möglichen daten-generierenden Prozessen sind Näherungsverfahren notwendig. MC FLO wendet den bekanntesten Algorithmus - Markov Chain Monte Carlo (MCMC) - an, welcher Stichproben aus der Posteriorverteilung zieht. Anhand des Beispiels wird ein exaktes Verfahren mit MCMC verglichen.
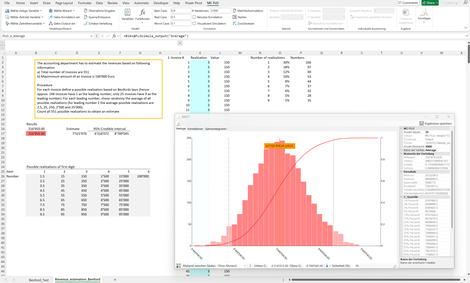
Benford_I: Anhand der Benford Verteilung wird aufgezeigt, ob Daten manipuliert wurden oder nicht. Hierbei auf den Bayes-Faktor abgestützt. Zusätzlich wird ein klassischer t-Test angewandt. Während der t-Test eine Manipulation der Daten für glaubwürdig hält, ist bei Anwendung des Bayes-Faktors keine Manipulation ersichtlich. Klingt paradox, ist es aber nicht. Leider wird bei der klassischen Statistik oft übersehen, dass der Verwerfungsbereich mit der Anzahl Stichproben korreliert. Je grösser die Anzahl Stichprobe ist, desto kleiner sollte das Signifikanzniveau sein.
Zusätzlich wird anhand weniger Informationen, hier der Anzahl Rechnungen und des maximalen Rechnungsbetrages, der Umsatz geschätzt.
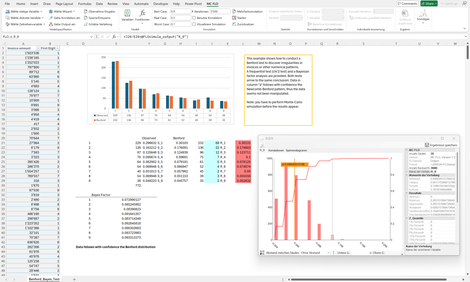
Benford_II: Anhand von 772 Rechnungen wird analysiert, ob die Daten einer Benford-Verteilung folgen.
Für die Prüfung wird der Bayes-Faktor angewandt. Dieser prüft die Nullhypothese - abgeleitet aus der Benford Verteilung - gegenüber allen anderen Hypothesen.
Bei 772 Rechnungen sollte die Zahl 9 als führende erste Zahl des Rechnungsbetrags ca. 35 mal vorkommen (4,5%), gemessen wurden aber 38 Vorkommnisse (4,9%). Zur Prüfung, ob die Abweichung von 0,4%-Punkten durch den Stichprobenumfang begründet werden kann, wird eine Beta-Binomialverteilung als Testverteilung herangezogen. Bei allen Zahlen ist eine Abweichung von der Benford-Verteilung nicht begründet.
Klassische Probleme und Lösungen

Birthday_problem: Klassisches Beispiel, welches aufzeigt, wie fehlerhaft der Mensch mit Wahrscheinlichkeiten umgeht.
Das Geburtstagsproblem legt dar, wie Übereinstimmungen öfters vorkommen, als vorher angenommen.
Hier: Wie hoch ist die Wahrscheinlichkeit, dass auf dem Fussballfeld (11 Spieler, 1 Schiedsrichter) zwei Personen am gleichen Tag Geburtstag haben?
Die meisten Menschen würden die Anzahl Personen durch die Anzahl Tage eines Jahres dividieren, um auf die gesuchte Grösse zu schliessen (23 / 365 = 13%), Mit einer Simulation können Sie den Sachverhalt spielerisch nachvollziehen. Lassen Sie sich überraschen.
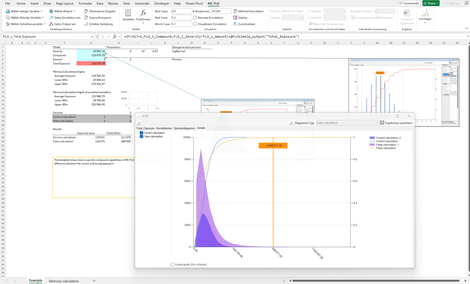
Compound_Function: Zeigt auf, wie unsichere Grössen -etwa Merkmalsverteilungen - korrekt multipliziert werden müssen. Dieser Vorgang wird auch als "Faltung" bezeichnet.
Leider werden fälschlicherweise beide Grössen multipliziert und das Resultat davon in die Ergebnisverteilung übernommen. Korrekt ist aber aus der Anteilsgrösse (Anzahl Fälle) ein fixer Wert n aus der zugehörigen Merkmalsverteilung zu nehmen und n mal eine Zufallszahl aus der anderen Merkmalsverteilung zu ziehen und diese zu addieren.
Beide Verfahren führen zu unterschiedlichen Verteilungen, auch wenn die Erwartungswerte in beiden Fällen gleich sind. Zur Differenzierung wird auf die Mehrfachsimulation zurückgegriffen. Ergänzend wird das richtige Vorgehen auch mit der ultra-schnellen Memory Calculation Engine vorgestellt.
Folgend sehen Sie hier, wie Sie die Investitionsbedarfsplanung mit Predictive Analytics bestimmen können. Das Muster können Sie für beliebige Bedarfsplanungen einsetzen.
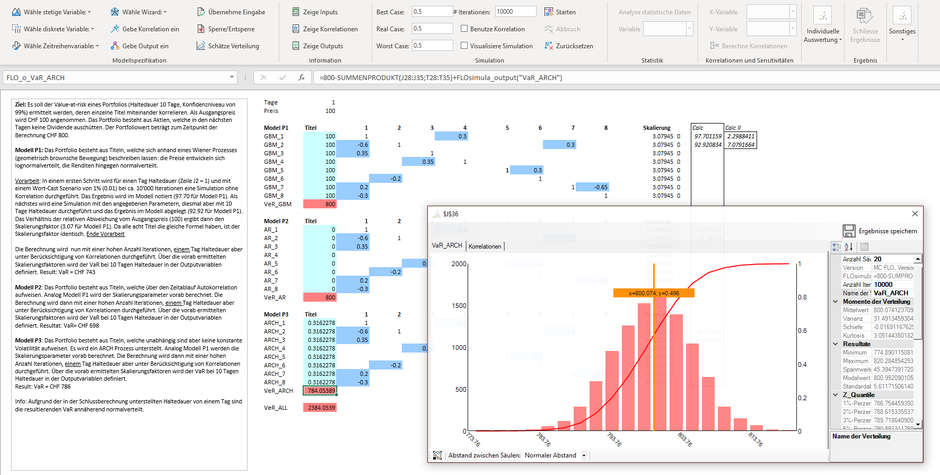
Hier zeigen wir Ihnen, wie Sie den Value-at-Risk bei Zeitreihenprozessen und unter Berücksichtigung von Korrelationen mit MC FLO ermitteln können. Sehen Sie hierzu unseren Blogbeitrag.
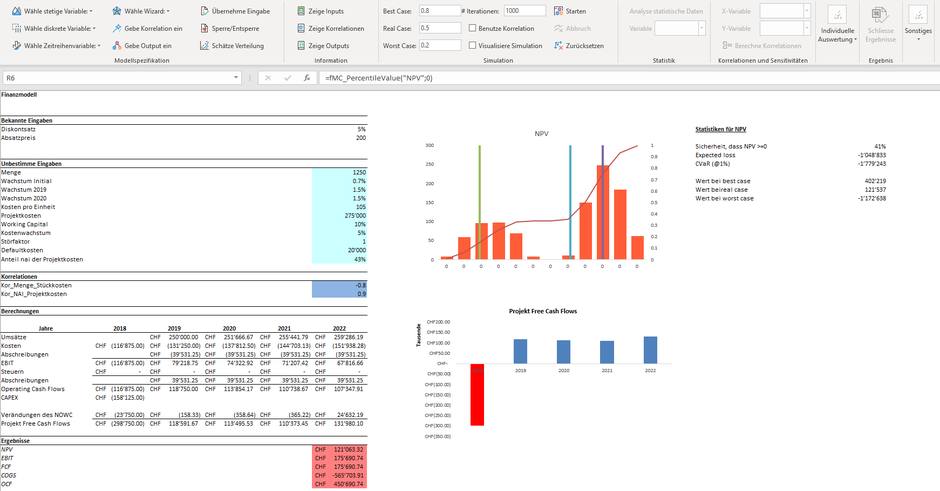
Folgend das mit MC FLO mitgelieferte Beispielprogramm einer Investitionsentscheidung, mit detaillierteren Angaben zum diskontierten Geldfluss (net present value - NPV), alles direkt in der Modellarbeitsmappe hinterlegt.