Nicht rechnen, simulieren – das Geburtstagsproblem

Auch wenn wir in unseren Blogs die Vorteilhaftigkeit der Simulation gegenüber dem Rechnen ausgiebig dargelegt haben, gibt es Bereiche, bei denen selbst Rechenkünstler an ihre Grenzen stossen und besser auf Simulationen zurückgreifen. Ein Paradebeispiel ist das Rechnen mit Permutationen.

Hierzu das bekannte Geburtstagsproblem: Auf einer Party befinden sich 23 nicht verwandte Personen. Wie hoch ist die Wahrscheinlichkeit, dass mindestens zwei dieser Gäste am gleichen Tag Geburtstag feiern? (Wir gehen davon aus, dass ein Jahr 356 Tage hat und keiner der Gäste an einem Schaltjahr geboren ist)

Eine gängige Suche über die bekannten Suchmaschinen bringt diverse Lösungen zum Vorschein, deren Zahlen das berühmte Permutationszeichen (!) zur Seite gestellt bekommen haben. Die Auflistung konkreter Formeln zur Lösung des Geburtstagsproblem möchen wir Ihnen ersparen, das ist uns alles zu kompliziert.

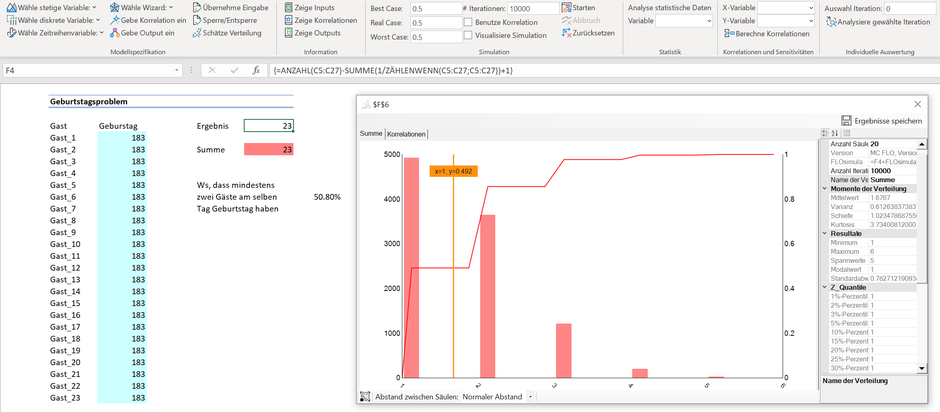
Im folgenden Excel haben wir unsere 23 Gäste aufgelistet, welche zwischen dem 01.01 (Tag 1) und dem 31.12 (Tag 365) Geburtstag haben können. Zelle F4 enthält eine Matrixformel von Excel, welches die Anzahl mehrfacher Einträge ermittelt. Sodann haben wir das Ergebnis einer Simulation mit 10'000 Iterationen dargestellt. So sehen wir, dass die Wahrscheinlichkeit (WS), dass mindestens zwei Gäste am gleichen Tag Geburtstag haben, über 50% beträgt! Tja, hätten Sie das Resultat erwartet?

Statt auf das Rechnen mit den für die meisten Menschen als schwierig empfundenen Permutationen abzustützen (so auch wir), reicht eine einfache Formel in Excel in Kombination mit einer Simulation aus, um zum Ergebnis zu gelangen.

Nun, das Geburtstagsproblem steht sinnbildlich für eine Vielzahl von Problemen, bei denen die Wahrscheinlichkeit falsch eingeschätzt wird.

Konkret, ganz analog: Stellen wir uns vor, dass eine Maschine aus 365 Teilen besteht und an 23 Standorten eine solche Maschine steht. Im Rahmen einer Qualitätskontrolle soll je Standort genau ein Teil einer Maschine einer Überprüfung unterzogen werden, wobei kein Teil mehrmals vorkommen darf. Würden Sie den jeweiligen Standortleitern-/innen den Auftrag erteilen, zufällig ein Teil auszuwählen? Mit der obigen Lösung zum Geburtsproblem wissen Sie nun, dass ein solches Vorgehen nicht ratsam ist.

Oder anders: Wenn Sie beim nächsten Fussballspiel darauf wetten, dass zwei Spieler der Startaufstellung beider Mannschaften (inklusive Schiedsrichter) an selben Tag Geburtstag haben, dann werden Sie mit einer Wahrscheinlichkeit von über 50% die Wette gewinnen. Viel Spass!