- Deutsch
- Español
- English
- Blog
- Get it now!
- Shop
- Wiki
- DEU - Stetige Verteilungen
- Gleichverteilung
- Dreiecksverteilung
- Normalverteilung
- LogNormalverteilung
- Betaverteilung
- Gumbelverteilung
- Gammaverteilung
- Exponentialverteilung
- Gekürzte Normalverteilung
- Weibullverteilung
- Pareto-Verteilung
- Cauchy-Verteilung
- ArcSin-Verteilung
- F-Verteilung
- Student-t-Verteilung
- chi2-Verteilung
- PERT-Verteilung
- Fréchet-Verteilung
- Logistische Verteilung
- DEU - Diskrete Verteilungen
- DEU - Zeitreihen
- DEU - Weitere Funktionen
- Referenz
- Umgang mit Variablen
- Interpretation
- Benutzerdefinierte Verteilung
- Begrenzte Verteilungen
- Korrelationen
- Memory Calculation
- Output
- Multiple Simulation / Box-Whisker
- Bayes-Faktor
- Forecast-Tool
- Batch-Funktion
- Datenanpassung
- Benford Analyse
- Dos and don'ts
- Bootstrap
- Decision Information Package
- Spider Diagramm
- Naive Bayes Klassifikation
- Risikomatrix
- DEU - Stetige Verteilungen
Datenanpassung über Verteilungsfunktion
Mit der Datenanpassung können Sie vorhandene Daten einer stetigen Verteilungsfunktion oder einer Zeitreihe zuordnen, mit dem Ziel, diese Funktion für eine Monte-Carlo Simulation nutzbar zu machen.
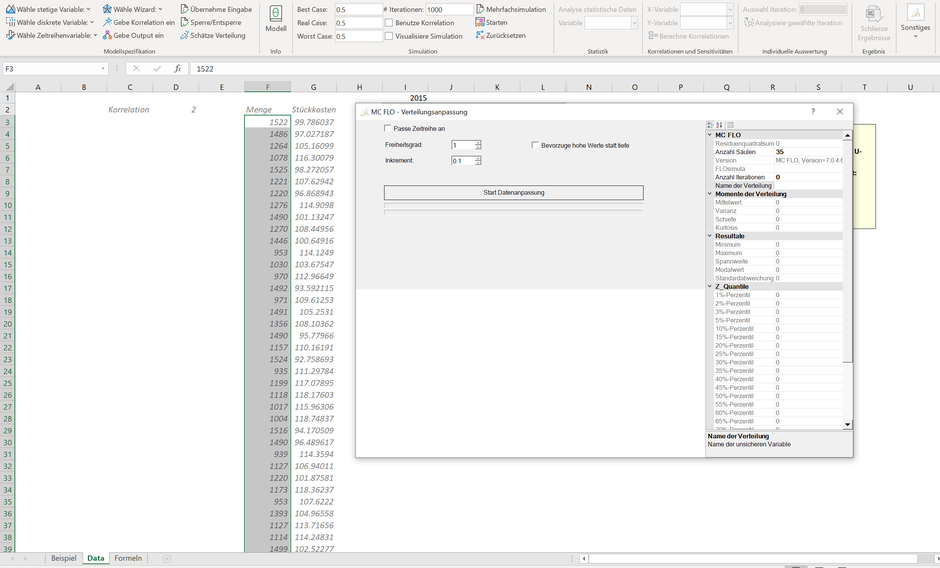
Ausgangslage der Datenanpassung sind Daten, welche zusammenhängend in Zellen in einer Microsoft Excel Datei vorliegen. Durch Markieren dieser Zellen und Aufruf von "Schätze Verteilung" öffnet sich der Wizard zur Datenanpassung.
Vorliegend werden die Daten aus Spalte F herangezogen. Durch Erhöhung des Freiheitsgrads (standardmässig auf 1 eingestellt) wird bei stetigen Verteilungen eine Erhöhung des Suchbereichs vorgenommen. Die Daten werden dabei besser auf einer der vorhandenen Verteilungen angepasst, die Berechnungszeit steigt aber mit Erhöhung des Freiheitsgrads. Mit der Erhöhung des Inkrements können Sie den Suchraum wiederum einschränken. Wir empfehlen Ihnen aber, dass Sie den Parameter Inkrement bei 0.1 belassen und nur beim Freiheitsgrad Anpassungen vornehmen.
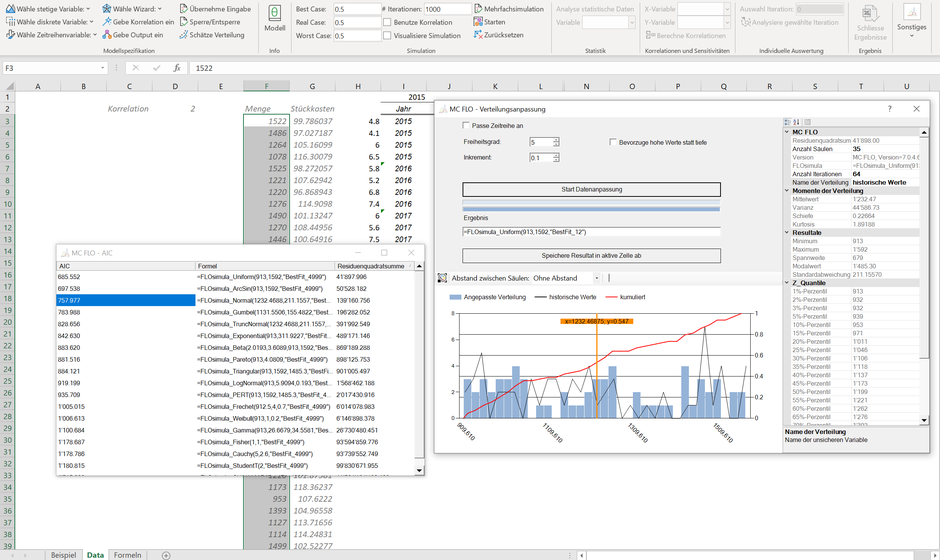
Nach Drücken von "Start Datenanpassung" wird die Anpassung vorgenommen. Folgend das Ergebnis nach einer Berechnung:
Als besten Schätzer hat MC FLO die Gleichverteilung ("Uniform") ermittelt und die entsprechende Formel bereits unter "Ergebnis" eingetragen. Mit Bestätigung über "Speichere Resultat in aktive Zelle ab" können Sie das Ergebnis in die aktive Zelle von Excel einfügen. Vergewissern Sie sich, dass Sie die richtige Zelle ausgewählt haben, da der Zellinhalt überschrieben wird. Über das Fenster mit der Bezeichnung "AIC" sehen Sie die verschiedenen Verteilungsfunktionen und ihre Performance in Bezug auf die Datenanpassung. So sehen wir, dass die Residuenquadratsumme bei der Gleichverteilung am geringsten ist, gefolgt von der ArcSin Verteilung. Gleiches gilt auch in Bezug auf das Akaide Informationskriterium ("AIC").
Weitere Informationen finden Sie im Handbuch.
Datenanpassung über Kerndichteschätzer
Das bisher dargestellte Verfahren zur Verteilungsanpassung setzt voraus, dass dezidierte Verteilungen und deren Formalisierung (im Sinne Verteilung x folgt der Funktion f(x)) vorliegen und somit nur die relevanten Parameter der Verteilung bestimmt werden müssen.
Im Gegensatz hierzu greifen nicht-parametrische Verfahren ausschliesslich auf die Daten zu, um hieraus die Verteilung zu generieren. Eine Verteilungsfunktion (f(x)) muss hier nicht formalisiert vorliegen. Ein Verfahren zur Bestimmung einer stetigen Verteilung, ohne Beizug einer Verteilungsfunktion stellt der Kerndichteschätzer dar.
Kernidee ist, dass die Beobachtungen (Daten) Dichten zugeordnet werden und aus der Summe der einzelnen Dichten (Kerne) die resultierende Verteilung gewonnen wird.
Stellen wir uns vor, dass folgende sechs Daten gemessen wurden: (-3, -1.1, -0.2, 1.5, 4.4, 5.8) und wir aus diese Daten die Verteilung f(x) generieren möchten.
Unten sind die einzelnen Datenpunkte (grau hinterlegt), die Kerndichte des ersten Punktes (Farbe orange, als Kern wird in MC FLO ein Gausskern mit Erwartungswert 0 und Standardabweichung 1 verwendet) und die resultierende Verteilung aus der Summe aller sechs Kerndichten (blaue Linie) bei einer Bandbreite von 0.1 ersichtlich.

Durch Variation der Bandbreite wird die Standardabweichung der Kerndichte angepasst. Eine Erhöhung der Bandbreite führt zu einer Erhöhung des Überschneidungsbereich der Kerndichten und somit zu einer Glättung der Verteilung. Die Auswahl einer optimalen Bandbreite ist je nach Datenlage komplex. Folgende Hilfestellungen können verwendet werden:
- wählen Sie eine geringe Bandbreite, falls genügend Daten vorhanden und diese relativ nah (kompakt) beieinander sind.
- wählen Sie hingegen eine grosse Bandbreite, falls nur wenige Daten vorliegen und diese weit auseinander fallen.
Folgend haben wir die gleichen Daten mit einer Bandbreite von 1.3 einer erneuten Kerndichteschätzung unterzogen, was in diesem Fall als genügende Approximation angesehen werden kann:

Wird, wie oben beschrieben, eine zu hohe Bandbreite gewählt (folgend bei 5), wirkt die resultierende Verteilung hingegen überglättet.
MC FLO stellt zwei Funktionen zu Berechnung des Kerndichteschätzers zur Verfügung:
- fmc_Kernel: Hierbei wird in Bezug auf die Ergebnisse der Simulation eine Schätzung der Verteilung f(x) für die ausgewählte Variable vorgenommen.
- fmc_Kernel2: Hierbei wird in Bezug auf konkrete Daten, welche in Excel hinterlegt sind, eine Schätzung der Verteilung f(x) für die ausgewählten Daten vorgenommen.
Der Vorteil von Kerndichteschätzer ist die Fähigkeit diskrete Verteilungen (etwa die Binomialverteilung) elegant in stetige Verteilungen zu überführen, welche dann in der Bayesschen Statistik als stetige Verteilung der Likelihood weiterverwendet werden kann.
Weitere Informationen zur Bayesschen Statistik können folgendem Blogbeitrag entnommen werden.