Bisher haben wir gelernt, wie die Bayes Formel auf Basis einer Simulation konkret angewendet werden kann. Dabei haben wir aufzeigt, wie wir unser Wissen anhand vorliegender Daten schärfen können. Diesen Prozess können wir dabei stetig wiederholen: Das geformte neue Wissen («A-posteriori») ist das «A-Priori» Wissen vor dem nächsten Lernprozess.
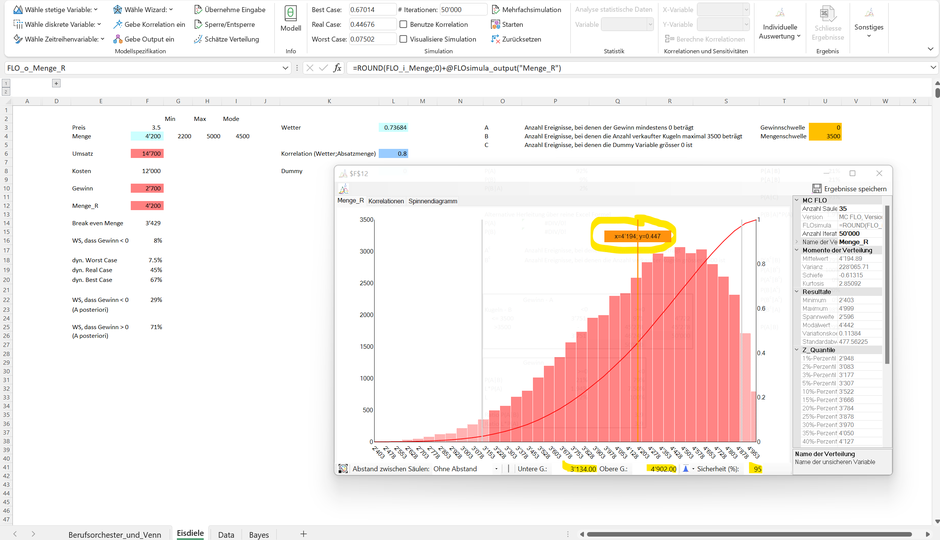
Fokussieren wir uns auf die Absatzmenge. Unser Vorwissen («A-Priori», Variable Menge_R) unterstellt, dass die Anzahl verkaufter Eiskugeln im nächsten Monat bekanntlich zwischen 2'200 und 5'000 Einheiten, mit einem wahrscheinlichsten Wert von 4'500 Einheiten, schwankt. Dies entspricht unsere Hypothese bezüglich der Absatzmenge (für die folgenden Ausführungen klammern wir die Korrelation mit dem Wetter aus).
Aus dieser Verteilung sind konsistente Aussagen ableitbar. Zur Abgrenzung hierzu bedient sich die Bayessche Statistik jedoch teilweise anderer Begrifflichkeiten als die frequentistische Statistik.
So können wir auf Basis unseres Vorwissens zu 95% sicher sein («glaubwürdiges Intervall», in Abgrenzung zum bekannten Vertrauensintervall), dass die Anzahl verkaufter Eiskugeln im nächsten Monat zwischen 3'134 und 4'902 Einheiten betragen wird. Analog kann argumentiert werden, dass die Wahrscheinlichkeit eine Absatzmenge weniger als 3'130 oder mehr als 4'906 zu Eiskugeln zu notieren, in Summe 5% ausmacht. Weiters ist ersichtlich, dass der Erwartungswert von ca. 4'196 Eiskugeln mit einer Wahrscheinlichkeit von ca. 55% überschritten wird.
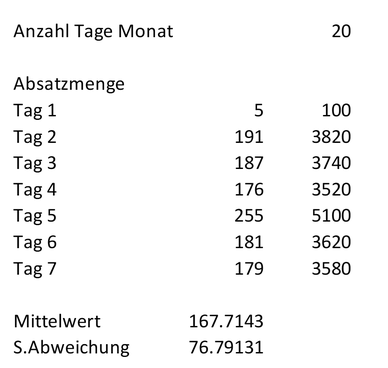
Nach 7 Arbeitstagen möchten wir ein erstes Fazit ziehen und basierend auf den Daten eine angepasste Prognose erstellen. Folgende Absatzmenge haben wir beobachten können (siehe Tabellenblatt «Data»):
Am Tag 1 wurden nur 5 Eiskugeln verkauft*, das Maximum wurde mit 255 Kugeln an Tag 5 erreicht. Wir möchten nun diese Daten nutzen, um unser Vorwissen anzupassen und daraus neues Wissen (A-posteriori) zu generieren. Wir haben bisher gelernt, dass:
«A-Posteriori» Wissen ∝ Likelihood * «A-priori» Wissen
Um aus den Daten zu lernen und somit unser A-posteriori Wissen zu formen, brauchen wir die Likelihood, also L(H|D) oder auch P(D|H), d.h., wir wollen wissen, welche Verteilung (Hypothese) mit den Daten kompatibel ist. Da wir nur eine Stichprobe der Daten (hier 7 Tage) haben, muss die Bayessche Statistik Annahmen bezüglicher möglicher Verteilungen machen, aus welchen die Daten stammen könnten. Ein Ansatz könnte dahin gehen, die Daten einer Normalverteilung zuzuordnen. Aus der Normalverteilung wissen wir, dass die Daten um den Mittelwert streuen und theoretisch unendliche Werte annehmen können.
Unsere planungsverantwortliche Person der Eisdiele vermutet, dass die verkauften Einheiten einer Arbeitswoche am ehesten mit der Hypothese einer Normalverteilung kompatibel ist, wobei sie zusätzlich annimmt, dass die Standardabweichung genau der Stichprobenabweichung entspricht (Zelle E13, wir bewerten diese Annahme hier bewusst nicht). Gesucht ist in diesem Fall der Erwartungswert der Normalverteilung, also L(Erwartungswert Normalverteilung | Umsatz aus 7 Arbeitstagen). Spätestens hier wird es dann sehr technisch, womit uns hier nur auf Worte beschränken wollen. Der Kern bleibt aber der gleiche: Der gesuchte Erwartungswert unserer Hypothese soll die grösste Wahrheitsnähe mit den Daten aufweisen. Es kann gezeigt werden, dass der gesuchte Erwartungswert genau dem arithmetischen Mittelwert der Stichprobe (Zelle E12) entspricht. Mit diesem Verfahren hätten wir die Verteilung eines einzelnen Tages identifiziert. Um zur Verteilung über den gesamten Monat (= 20 Arbeitstage) zu kommen, ist die gemeinsame Verteilung über das Produkt jeder einzelnen Verteilung herzuleiten. Dieses Verfahren – auch als Compounding oder Convolution bekannt - zeigen wir gleich…
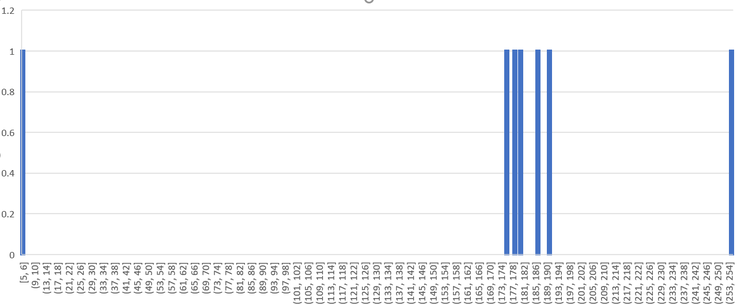
Aber vorab noch einmal die provokative Frage: warum ist eine Normalverteilung der Daten angemessen und was spricht dagegen? Wir wagen über den Begriff der Wahrheitsnähe einen erneuten Versuch, dies auch um den technischen Begriff der Likelihood zu umgehen. Im Kern geht es darum einzusehen, dass wir mit der Wahl unserer Entscheidungen immer falsch liegen, einige sind hingegen näher an der Wahrheit als andere. Schauen wir uns die Daten aus den 7 Arbeitstagen noch einmal an. Hierzu haben wir jeden einzelnen Datenpunkt als eigenständige Säule in einem Histogramm abgebildet (auf der y-Achse ist die Anzahl Treffer (jeweils 1) und auf der x-Achse die Anzahl Eiskugeln abgetragen).
Die Daten lassen prima vista eher darauf schliessen, dass hier keine Normalverteilung vorliegt. Fünf Datenpunkte liegen relativ nah – zwischen 176 und 191 - beieinander, zwei Datenpunkte sind wie oben dargestellt aber weit von diesen entfernt. Ist diese Datenausprägung darauf zurückzuführen, dass die Daten einer anderen Verteilung - etwa einer Student-T Verteilung - folgen, oder ist das Gesehene doch auf die Stichprobenvariabilität zurückzuführen? Abschliessend können wir das nicht festlegen und wir wollen das auch gar nicht. Immerhin, die verantwortliche Person der Eisdiele kann mit einem Trick diese Fragestellung und die davon abgeleiteten Probleme umschiffen.
Die Idee besteht darin, die Daten so zu nehmen wie sie sind («let the data speak») und daraus die Daten für den gesamten Monat zu bestimmen. Hierzu haben wir die Stichprobe der Daten analog oben in ein «Histogramm» überführt (siehe Zeile I3ff.) und die Anzahl Säulen auf 7 beschränkt. Jeder der Daten zwischen 5 und maximal 255 Eiskugeln wird einer eigenen Säule zugeordnet.
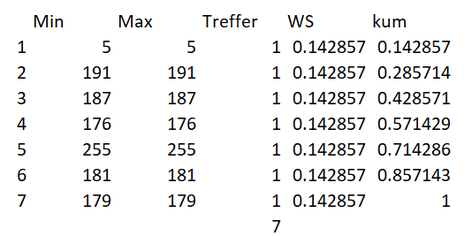
Unter der Spalte WS haben wir die Wahrscheinlichkeiten, gemessen an der Stichprobe, abgetragen. So beträgt die Wahrscheinlichkeit 5 Eiskugeln zu verkaufen, ca. 14.2%. Angesichts dessen, dass alle sieben Datenpunkte der Stichprobe disjunkt sind, trifft dies für alle verkauften Eiskugeln zu: da 191 Eiskugeln nur einmal verkauft wurden; beträgt die Wahrscheinlichkeit ebenfalls 1/7 = ca. 14.2%. In der letzten Spalte haben wir die kumulierte Wahrscheinlichkeit (kum) für die möglichen Bereiche abgetragen. Diese beträgt in Summe eins.
Der erste Schritt in unserem Trick besteht darin, aus dieser Stichprobe wiederholt weitere Stichproben mittels «bootstrapping» zu ziehen. Daran anknüpfend ist sodann die Summe der Ergebnisse zu bilden, was dem «Compounding» oder «Convolution» entspricht. Doch der Reihe nach.
Nehmen wir an, dass wir eine Vorhersage für sechs Tage (statt der im Modell unterstellten 20 Tage) auf Basis der bisherigen Stichprobe machen müssten: Wie hoch wird die Anzahl der verkauften Eiskugeln über alle sechs Tage wohl sein? Welche Werte werden eher wahrscheinlich sein, welche weniger? Wir wählen einen Zufallsgenerator, der uns ein Zahl zwischen 0 und 1 würfelt. Liegt die gezogene Zahl etwa zwischen 0.14 und 0.28 werden 191 Eiskugeln für die verkaufte Menge am ersten Tag gezogen (entspricht «Urnentyp 2»). Dieses Verfahren wird nun für die weiteren fünf Tage durchgeführt. Mit jeder weiteren Stichprobe müssen wir die Summe bilden, um die Anzahl der Eiskugeln über die sechs Tage zu bestimmen. Da die ursprüngliche Stichprobe die meisten Beobachtungen zwischen 176 und 191 Eiskugeln aufwies, sollte die Wahrscheinlichkeit, dass an sechs aufeinanderfolgenden Tagen 255 Eiskugeln verkauft werden (in Summe müsste dies 1'530 Eiskugeln entsprechen), sehr gering ausfallen.
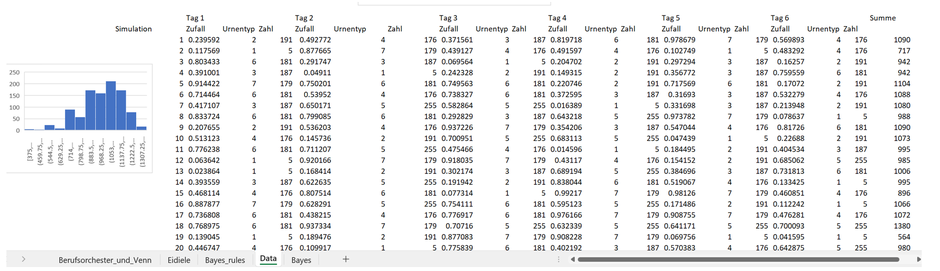
Anbei das Ergebnis - nur auf Excel Funktionen abstützend - einer Simulation mit 1’000 Iterationen und der entsprechenden Verteilung der Anzahl Eiskugeln (gezeigt werden nur die ersten 20 Simulationsergebnisse, im Excel File ist die gesamte Herleitung ersichtlich, siehe Tabellenblatt «Data»). So sehen wir, dass die erste Simulation einen Wert von 1'090 Eiskugeln errechnet, aus der zweiten Simulation resultiert ein Wert von 717 Eiskugeln, usw., siehe Daten unter Spaltenbezeichnung «Summe»)
Die resultierende Verteilung ist dann – ohne Abstützen auf eine bestimmte Verteilung und deren Parameter - unsere Likelihoodverteilung. Dadurch, dass Sie die Daten direkt genommen haben, ist die grösste Wahrheitsnähe gegeben.
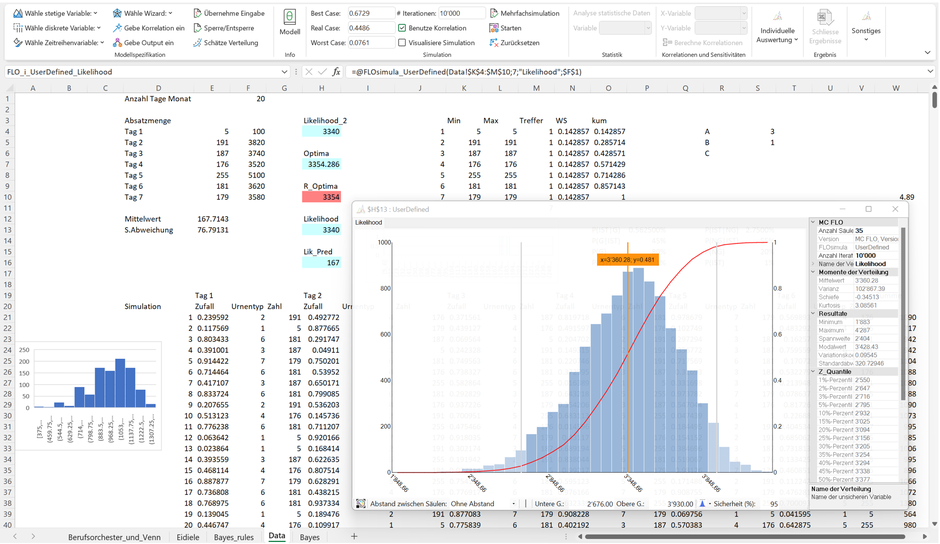
Anbei die Likelihoodverteilung für unsere Eisdiele, hergeleitet über das bootstrap Verfahren:
Tipp: Falls sich nicht nur allein auf die bestehenden Daten abstützen möchten, können Sie durch Variation der Anzahl Säulen des Histogramms quasi auf Knopfdruck neue Zahlen zwischen den Minimum und dem Maximum generieren, ohne die Struktur der Daten grundlegend zu verändern. Eine solche angepasste Likelihood haben wir in Zelle H4 vorgenommen.
Nun müssen wir noch unsere hergeleitete Likelihood mit unserem Vorwissen kombinieren. Da wir in Bezug auf das Vorwissen als auch in Bezug auf die Likelihood von Verteilungen ausgehen, erfordert die Kombination das Abstützen auf bestimmte Algorithmen, welche ohne Kenntnis der resultierenden Verteilung in der Lage sind, von dieser eine Stichprobe zu ziehen**. Exemplarisch für eine solche Klasse von Algorithmen ist die Verwendung von Monte-Carlo Markov Chain (MCMC) Verfahren, wie der in MC FLO implementierte Metropolis Hastings Algorithmus (Details zur Vorgehensweise können dem oben zitierten Onlinebuch entnommen werden, siehe Kap. 7).
Wie bereits dargestellt, reicht es wenn wir unser A-posteriori Wissen als proportional zum Produkt der Likelihood und unserem Vorwissen auffassen.
«A-Posteriori» Wissen ∝ Likelihood * «A-priori» Wissen
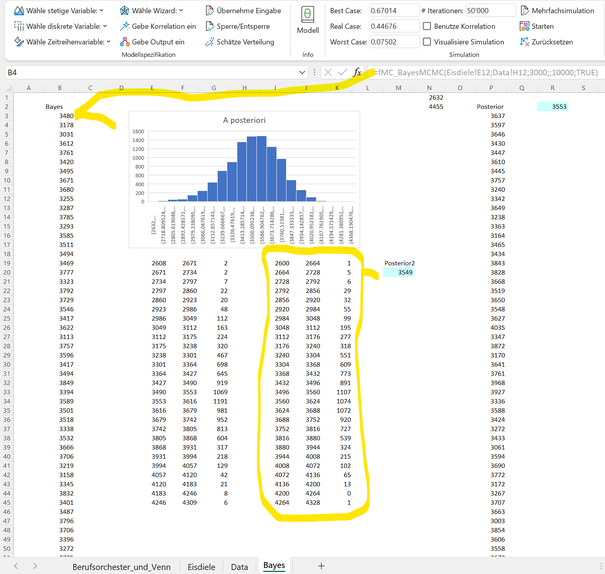
Anbei das Resultat der Kombination von Likelihood und Vorwissen, hergeleitet mit der entsprechenden MCMC Formel von MC FLO (die in Zellen B3ff. aufgeführten Zahlen entsprechen der gezogenen Stichprobe der in Zelle B3 über eine Matrix Formel eingegebene MCMC Funktion; alternativ kann auch ein Histogramm ausgegeben werden, welches unten im gelb umrandeten Rahmen wiedergegeben ist; wir empfehlen das Ergebnis der fmc_MCMC Formel separat abzulegen und von dieser die benutzerdefinierte Verteilung zu erzeugen).
Es ist Zeit für eine erste Zusammenfassung.
Zur Vorhersage der Anzahl verkaufter Eiskugeln für den nächsten Monat haben wir uns zu Beginn auf Vorwissen oder allgemein einer Einschätzung abgestützt und dieses Vorwissen anhand einer PERT-Verteilung formalisiert. Nach sieben Tagen haben wir die bis dahin vorliegenden Daten herangezogen, um daraus die bestmögliche Verteilung für den Monat herzuleiten («Likelihood»). Schliesslich haben wir Vorwissen und Daten kombiniert, um daraus unser Wissen neu zu formen. Dieses Wissen liegt ebenfalls als Verteilung vor («A-Posteriori» Verteilung).
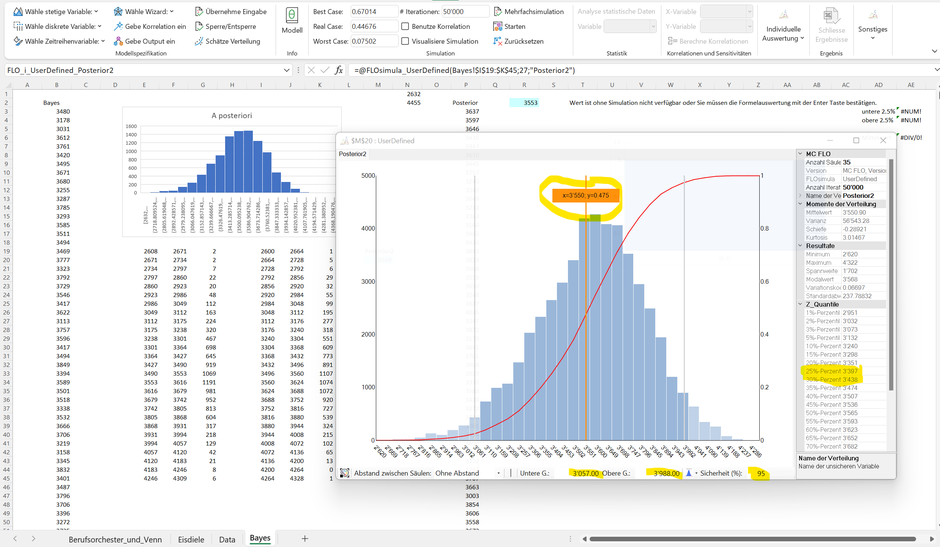
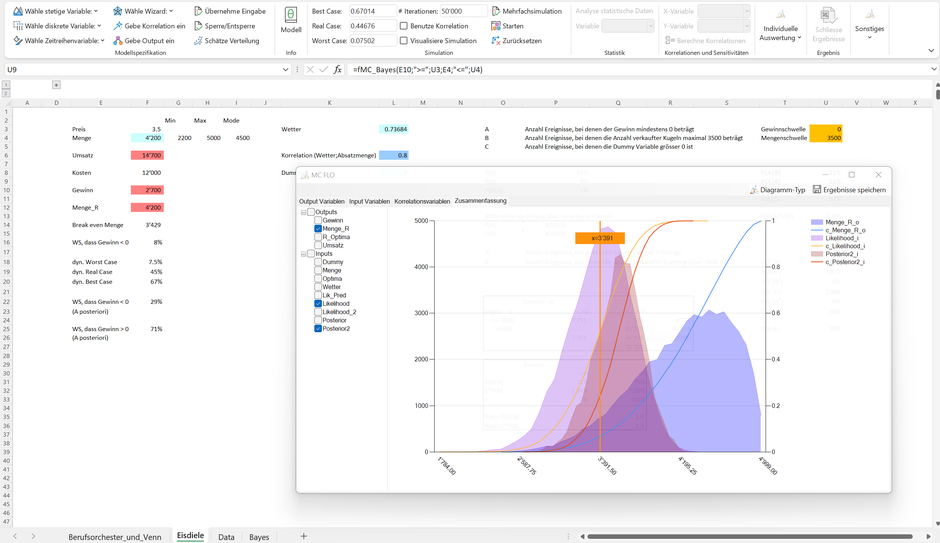
Aus der A-Posteriori Verteilung leiten wir ab, dass im Erwartungswert ca. 3'550 verkaufter Eiskugeln für den Monat prognostiziert werden. Mit 95% Sicherheit («glaubwürdiges Intervall») gehen wir davon aus, dass die Anzahl verkaufter Eiskugeln zwischen 3'057 und 3’988 Eiskugeln schwanken wird. Die Schwankungen sind Zeichen der Unsicherheit, welche die Bayessche Statistik bereits mit Erstellen des Vorwissens berücksichtigt hat.
In Bezug auf die Frage, wie hoch die Wahrscheinlichkeit sein wird nächsten Monat einen Gewinn zu erwirtschaften, haben wir mit den bisherigen Berechnungen alle notwendigen Daten bei Hand. Wir haben angenommen, dass die Kosten bei 12'000 CHF pro Monat liegen. Gesucht ist somit die Menge aus der A-posteriori Verteilung, welche bei gegebenem Preis von 3.50 CHF pro Eiskugel zu einem Gewinn führt. In unserem Fall sind es 3'429 Eiskugeln (12'000 / 3.50). Wir suchen somit nach der Wahrscheinlichkeit, dass die abgesetzte Menge im nächsten Monat grösser gleich 3'429 Eiskugeln liegt. Aus der obigen Graphik ist ersichtlich, dass 3'429 zwischen dem 25% und 30% Perzentil liegt. Sprich, zwischen 70% und 75% der Daten liegen oberhalb der Gewinnschwelle von 0 (im Tabellenblatt «Eisdiele» ist der genaue Wert von 71% in Zelle F35 ersichtlich).
Noch einmal ein «Wow»: Mit Erstellung des Modells und auf Basis unseres Vorwissens haben wir eine Wahrscheinlichkeit, dass der Gewinn kleiner Null ausfallen wird, von 8% ermitteln können. Unter Zugrundelegung der Daten haben wir unser Wissen neu formen können. Aus der A-posteriori Verteilung folgt nun, dass die Wahrscheinlichkeit, ein Gewinn kleiner Null auszuweisen, auf 29% gestiegen ist.
Unten haben wir die jeweiligen Verteilungen (Menge_R als A-priori Verteilung, Likelihood und A-Posteriori) dargestellt. Wir ersichtlich, fügt sich die A-posteriori Verteilung zwischen der A-priori und der Likelihood Verteilung ein.
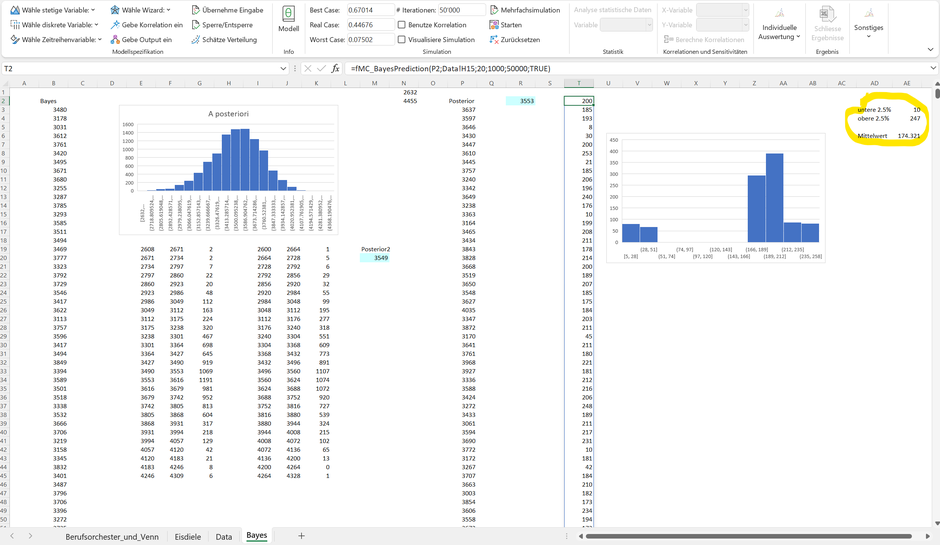
Die Bayessche Statistik geht aber noch einen Schritt weiter. So können wir auf Basis unseres A-Posteriori Wissens und der Likelihood der gemessenen 7 Arbeitstage eine Prognose für die nächsten 7 Arbeitstage erstellen. Mit der «fmc_BayesPrediction» Formel ist dies ein Kinderspiel. Folgend haben wir in Zelle T2 des Tabellenblatts eine solche Vorhersage auf Basis von 1'000 Simulationen erstellt.
Gegen Ende wollen wir die Daten rein mit Excel-Funktionen analysieren. So sehen wir, dass das glaubwürdige Intervall von 95% eine Untergrenze von 10 Eiskugeln und eine Obergrenze von 247 Eiskugeln umfasst. Oder anders: es gibt jeweils eine knapp 2.5%-ige Wahrscheinlichkeit, dass weniger als 10 Eiskugeln und mehr als 247 Eiskugeln an einem Tag in den nächsten sieben Arbeitstagen verkauft werden.
Fazit: Die Bayessche Statistik ist abseits des in heutiger Zeit prominent beigezogenen Vergleichs, ob eine Corona Impfung sinnvoll ist oder nicht, auch für die Unternehmensplanung – und Steuerung ein hilfreiches Instrument, um Daten mit Wissen zu kombinieren und aus der vereinten Kraft beider neue Schlüsse zu ziehen.
P.S.: Wie immer haben versucht die Beispiele so einfach und die Zahlen so klein wie möglich zu halten. Wir können daher durchaus nachvollziehen, wenn Eisdielen mit den hier dargestellten Umsätzen auf eine Monte-Carlo Simulation und den Beizug der Bayesschen Statistik verzichten 😊.
Für weitere Fragen stehen wir Ihnen unter support@mcflosim.ch gerne zur Verfügung.
* Es kann immer etwas schief laufen. Im Idealfall ist dies bereits bei der Schärfung des Vorwissens berücksichtigt, etwa indem die Mindestabsatzmenge entsprechend angepasst wird.
** Einige Autoren gehen sogar einen Schritt weiter und bestimmen anhand einer speziellen Bootstrap Technik die A-Posteriori Verteilung direkt, siehe Trevor Hastie, Robert Tibshirani, Jerome Friedman: The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Seite 271, abrufbar unter Elements of Statistical Learning: data mining, inference, and prediction. 2nd Edition. (su.domains)
P.S.: Wie immer gilt: Wenn Sie die Simulation immer und immer wieder vollziehen, werden die Ergebnisse jeweils - je nach Anzahl Iterationen pro Simulation - leicht abweichen. Aus diesem Grund und weil wir die Berechnungen mehrmals durchgeführt haben, erscheinen nicht immer die gleichen Zahlen und Aussagen wie im Text dokumentiert.
Weitere Informationen können aus dem Onlinebuch «Probability and Bayesian Modeling» von Jim Albert und Jingchen Hu; Probability and Bayesian Modeling (bayesball.github.io), «Bayessche Statistik in der Risikoquantifizierung» von Prof. Dr. Gabriele Wieczorek und Oliver Disch (erschienen im Risiko Manager 10/2019 und «Wahrscheinlichkeiten, Bayes-Theorem und statistische Analysen» von Prof. Dr. Werner Gleißner, erschienen im Controller Magazin 02/2014, entnommen werden. Die erwähnten Artikel sind Online aufrufbar.
Das Excel finden Sie hier.

Kommentar schreiben