Der Fluch der Mittelwerte

Tagtäglich strömen Informationen und Zahlen über uns herein, welche gefiltert und sortiert werden müssen, damit sinnvolle Entscheide getroffen werden können. Dabei wird – meist unbewusst - eine Vereinfachung vorgenommen. Zahlen in Bezug auf einen abgrenzbaren Sachverhalt werden oftmals vereinfacht als Mittelwert wiedergegeben; sei es bei wirtschaftlichen Themen (Nachfrage, Investitionen, Kapazität) oder auch naturwissenschaftlichen-technischen Ausführungen (Wassertiefe, Luftdruck). Anhand der Geschichte des Betrunkenen zeigen wir Ihnen, zu welchen Fehlschlüssen Vereinfachungen führen und warum im Zuge der fortschreitenden Digitalisierung auf eine solche verzichtet werden kann.

 
Stellen Sie sich einen Betrunkenen vor, der die Mittellinie entlang einer viel befahrenen Landstrasse folgen soll. Er wird auf seinem Weg mal nach links und mal nach rechts von der Mittellinie abschweifen. Im Durchschnitt wird er auf der Mittellinie gelaufen sein, dies obwohl er diese nur punktweise (bei Kreuzung) berührt haben dürfte. Die Schlussfolgerung müsste somit lauten, dass der Betrunkene den Spaziergang unbeschadet überlebt hat. Sie ahnen es wohl schon. Wenn jedoch davon auszugehen ist, dass der Betrunkene nach einer Weile von einem Auto erfasst wird, wird er das Ziel nicht erreichen. Stellen Sie sich zudem vor, dass mehrere Betrunkene nacheinander diesen Spaziergang unternehmen. Auf dem Weg wird einer mal nach 100 Meter, der andere nach 200 Metern von einem Auto erfasst. Auf der Strecke von 800 Metern kommt mitunter keiner ans Ziel. Obwohl im Mittel alle Betrunkenen die Mittellinie entlanggelaufen sind, sind im Mittel alle nicht angekommen. Komisch, nicht wahr?  

Der Fluch der Mittelwerte steht für dieses Paradoxon. Aus einer vorab vorgenommenen Verdichtung von Informationen werden falsche Schlüsse gezogen und somit Fehlentscheidungen begünstigt. Anderes Beispiel? Sie planen den Verkauf eines neuen Produktes. Sie sind sich sicher, dass die Nachfrage zwischen 50'000 und 150'000 Einheiten im nächsten Jahr betragen wird. Im Mittel gehen Sie von 100'000 Einheiten aus. Pro verkaufter Einheit beträgt der Gewinn immer 10 CHF. Also müssen im nächsten Jahr 10 MCHF Gewinn resultieren, oder? Tja, wenn Sie diese Rechnung ohne den Produktionsverantwortlichen gemacht haben, dann wird das nicht aufgehen. Wenn die Fabrik die Produktionskapazitäten auf die Nachfrage von 100'000 Einheiten ausgerichtet hat, dann können minimal 50'000 und maximal 100'000 Einheiten verkauft werden. Also im Mittel nur 7.5 MCHF Gewinn. So einfach.

Diese Beispiele zeigen auf, dass das Abstützen auf eine konkrete Zahl – etwa den Mittelwert – zu fatalen Schlüssen führen kann. Mit der Digitalisierung ist eine solche drastische Filterung nicht notwendig, da genügend von Mensch geschaffene Instrumente zur Seite stehen, um Entscheidungen auch auf Basis umfassenderer Informationen treffen zu können. Mehr noch, wer sich dieser Informationen behelfen kann, hat einen Vorteil. Oder anders ausgedrückt: auf Basis einer Zahl sollten Sie keinem mehr trauen!

In vielen Beiträgen haben wir anhand von Simulationen dargelegt, dass eben nicht die Mittelwerte – oder vereinfacht ein Punktwert - als Entscheidungskennzahl herangezogen werden sollten, sondern die Bandbreite möglicher Realisationen unter Einschluss der Wechselwirkungen als Massstab zu nehmen sind. 

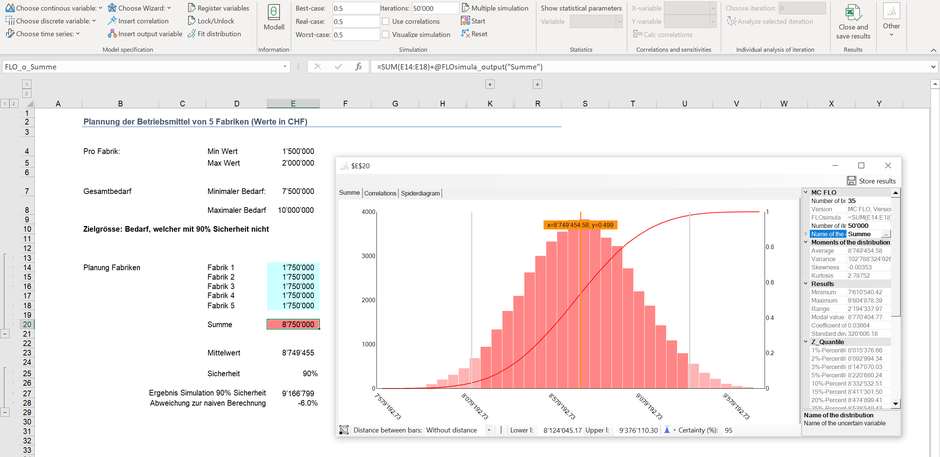
Ein ähnliches Phänomen des Fehlschlusses geht auf den Fluch der Extremwerte zurück. Und da wir bisher noch kein Beispiel ins Spiel gebracht haben, möchten wir sofort loslegen. Stellen Sie sich vor, dass das Betriebsmittelbudget für das nächste Jahr geplant werden soll. Das Budget setzt sich aus den gemeldeten Kosten von 5 Fabriken zusammen, wobei jeweils Kosten zwischen 1.5 MCHF und 2 MCHF anfallen. Dabei unterstellen wir, dass die Kosten gleichverteilt sind. Das Management soll das Betriebsbudget so aufstellen, dass mit 90%-iger Sicherheit eine Budgetüberschreitung verhindert wird. Jede Fabrik kommuniziert somit 1.95 MCHF, was in Summe ein Betriebsbudget von 9.75 MCHF ergibt. Denken Sie etwa, dass hier etwas falsch läuft?

Sehen wir das Ganze nach einer Simulation an: Siehe da, das Gesamtbudget bei einer 90%-igen Sicherheit beläuft sich nur noch auf ca. 9.16 MCHF – also um knapp 600 TCHF tiefer als die Summe der einzelnen Meldungen. Sehen wir uns die resultierende Grösse grafisch an, erkennen wir, dass die möglichen Ergebnisse einer Normalverteilung folgen, obwohl die individuellen Verteilungen je Fabrik als Gleichverteilung unterstellt worden sind. Dies folgt automatisch aus dem zentralen Grenzwertsatz, der hier die volle Wirkung zeigt. 

Falls bei Ihnen die Budgets in den letzten Jahren nicht ausgeschöpft wurden, haben Sie nun eine mögliche Erklärung zur Hand. Mehr noch, wenn Sie zukünftig Simulationen nutzen, können Sie das bei der Budgetierung eingesparte Geld für sinnvollere Massnahmen einsetzen.

P.S.: Einige Beispiele sind dem Buch von Sam L. Savage: «The Flaw of Averages: Why We Underestimate Risk in the Face of Uncertainty» entnommen. Die entsprechenden Copyright-Rechte gelten uneingeschränkt.