In einem unserer letzten Blogs haben wir das quantitative Portfoliomanagement für Investitionen (capital budgeting) anhand eines einfaches Beispiels aufgezeigt. Dabei wurde festgehalten, dass mit zunehmender Anzahl von möglichen Investitionsalternativen die Anzahl von Kombinationen rapide ansteigt. Eine Zusammenstellung von 10 möglichen Investitionsprojekten, welche bereits in mittelständischen Unternehmen umgesetzt werden dürften, mündet in über 1'000 möglichen Kombinationen. Sind es 11 Investitionsprojekte, sind es bereits über 2'000 Kombinationen. Hier über Excel diese herauszuschälen und als mögliche Variablen in MC FLO zu hinterlegen, kam bisher einer Mammutaufgabe gleich.
Mit den als Matrixformel implementierten Funktionen (ab MC FLO Version 7.2.5.1):
- fmc_PortfolioCombn(«AValue»): Bestimmt die Anzahl Kombinationen (ohne Wiederholung, ohne bestimmte Reihenfolge) von n («AValue») Titeln eines Portfolios.
- fmc_PortfolioMatrix(«aMatrix», «AsInput»): Bestimmt die Möglichkeiten zur Bildung eines Portfolios mittels Matrixfunktion, bei der n Titel ausgewählt werden. Die Ausgabe ist eine n x 2 Matrix, bei der die erste Spalte die berechneten MC FLO Variablen und die zweite Spalte die Namen enthält. Falls AsInput = WAHR (1), dann werden die berechneten MC FLO Variablen als Inputvariablen hinterlegt, ansonsten als Outputvariablen.
- fmc_PortfolioCorrMatrix((«aMatrix», «FillRandom»): Bestimmt die Korrelationsmatrix eines Portfolios aus n Titeln. Resultat ist eine q x 1 Matrix. Falls «FillRandom» = WAHR (1), dann wird jede Korrelationsbeziehung mit einem zufälligen Wert zwischen -0.3 und +0.3 hinterlegt, andernfalls mit dem Wert 0.
können wir an den Sachverhalt viel gelassener herangehen.
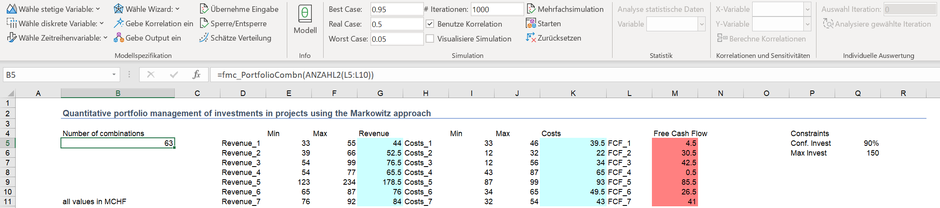
Im folgenden Excel-Beispiel sind diese Funktionen zur Bestimmung eines optimalen Portfolios, wobei 7 (sieben) verschiedene Anlagen kombiniert sind, herangezogen.
Als erstes gilt es das Portfolio isoliert für jeden einzelnen Investitionsfall aufzubauen. Hierzu haben wir die unsicheren Ergebnisse in Bezug auf den Cash-Flow relevanten Umsatz (Spalte G) und die Cash-Flow relevanten Ausgaben (Spalte k) als unsichere Variablen abgetragen; die Differenz beider Grössen entspricht dem Free Cash Flow der jeweiligen Projekte (Spalte K), alles in MCHF.
Bei der Portfoliobildung von Investitionen sind im Regelfall Nebenbedingungen zu berücksichtigen, etwa die verfügbaren Mitarbeiter oder finanzielle Beschränkungen, welche durch das Budget vorgegeben sind. In Zelle Q6 geben wir vor, dass maximal 150 MCHF (bei 90% Konfidenz) für die Investitionen zur Verfügung gestellt werden können. Welche Kombinationen sind heranzuziehen, um den Free-Cash-Flow bei minimaler Varianz zu maximieren?
Unsere Aufgabe besteht also darin ein Portfolio zusammensetzen, das den Kehrwert des Variationskoeffizienten (Verhältnis aus erwartetem Free Cash Flow zur Standardabweichung) maximiert und dabei das Investitionsdach von 150 MCHF mit einer Sicherheit von 90% nicht überschreitet.*
In einem ersten Schritt tragen wir alle möglichen Portfoliokombinationen und deren Kosten in einem separaten Tabellenblatt ("Idee") ein. Wir extrahieren die Inhalte aus der Matrixformel und fügen diese dann als Text in separaten Spalten ab, womit wir die einzelnen Werte auslesen und analysieren können. Von diesen Werten löschen wir alle Portfoliokombinationen, deren Ausgaben im Erwartungswert über die vorgegebenen 150 MCHF liegen. Aus den verbleibenden Portfoliokombinationen (42) bilden wir MC FLO Variablen, welche für die Optimierung heranzuziehen sind.
Investitionen sind im Regelfall nicht unabhängig. Wird mehr in manuelle Prozesse investiert, sollten Investitionen in Softwareprojekte für die gleichen Prozesse eher abnehmen. Bei 7 Projekten sind es potentiell 21 Korrelationsbeziehungen, welche bei der Modellbildung zu berücksichtigen sind. Auch hier bietet es sich an, mit MC FLO die relevanten Beziehungen als Schablone zu hinterlegen, die dann mit den Korrelationskoeffizienten nur noch befüllt werden müssen (die Herleitung eines angemessenen Korrelationskoeffizienten ist - im Gegensatz zu den projektindividuellen Kenngrössen - oftmals nur im Zusammenspiel aller involvierten Projektleiter möglich).
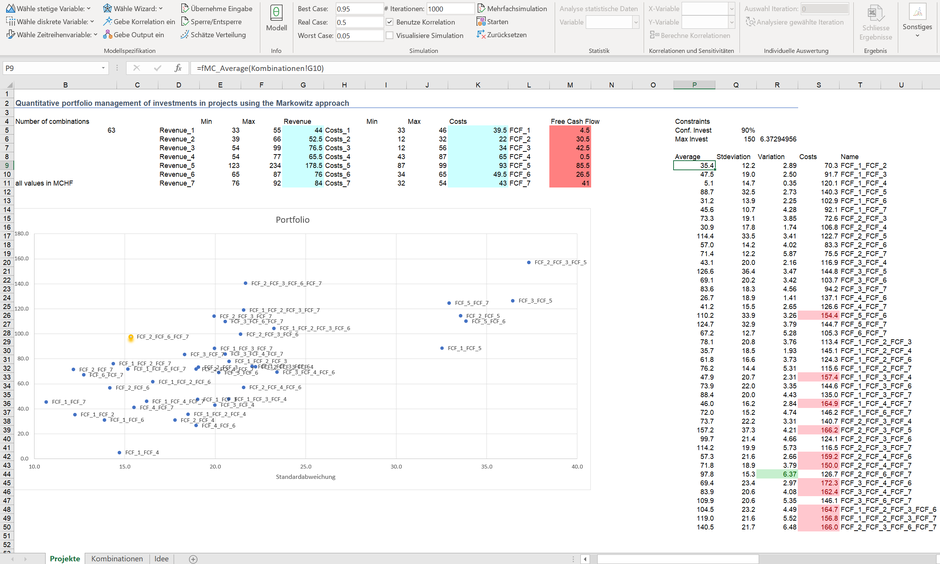
Das war es. Es liegen nun alle Informationen vor, mit der die Monte-Carlo Simulation angestossen werden kann. Im Folgenden ist das Resultat der Portfoliooptimierung ersichtlich.
Das optimale Portfolio, welches die Investitionsbeschränkung von 150 MCHF bei 90% Konfidenz (Sicherheit) einzuhalten vermag und den höchsten Koeffizienten ausweist, ist aus den Projekten 2, 6 und 7 zusammengesetzt. Jede andere Kombination (aus den 127 mathematisch möglichen) sollte hingegen ausgeschlossen werden.
Excel ermöglichst selbst in der aktuellsten Version (Stand 22.06.2020) nur knapp 1 Mio. Zeileneinträge, was den hier vorgestellten Ansatz auf 20 Investitionsprojekte und deren Kombinationen beschränkt. Aber auch mit hunderten von Projekten ist eine relativ rasche Lösung mit Excel und MC FLO möglich. Dazu müssen Sie aber das berühmte "Teile und herrsche" Prinzip anwenden. Eine Strategie besteht darin, dass Sie etwa 20 Projekte (deren Korrelationen abschliessend sein sollten) auswählen, diese mit dem hier vorgestellten Ansatz analysieren und das Resultat davon wieder als Ausgangslage für eine erneute Portfoliobildung nehmen.
Viel Spass bei der Portfoliobildung!
*Neben dem Variationskoeffizienten können auch andere Bewertungskennzahlen herangezogen werden, etwa der Free Cash Flow@Risk; dieser setzt nicht auf den symmetrischen Begriff der Standardabweichung auf.


Kommentar schreiben