Wer die letzten Blogbeiträge gelesen hat, wird festgestellt haben, dass Korrelationen bei der Simulation ein wichtiges Instrument zur Entscheidungsfindung darstellen. Die Beziehung zwischen Umsatz und Preis bei der Umsatzplanung verdeutlicht, dass im realen Alltag Menschen auf Veränderungen reagieren. Korrelationen können in diesem Kontext auch als Ausprägung simulierter Preiselastizitäten aufgefasst werden (nicht jeder Kunde reagiert auf eine Preisanpassung gleich). Diese möglichen Veränderungen sind in der Planung zu antizipieren.
Bevor wir auf eine weitergehende grafische Interpretation der Korrelation eingehen, verweisen wir auf eine Einführung in die Korrelationsanalyse, welche wir in diesem Blogbeitrag zusammengestellt haben. Es ist in Erinnerung zu rufen, dass der hier betrachtete (Pearson-)Korrelationskoeffizient eine dimensionslose Zahl darstellt, welcher zwischen -1 und +1 liegt. Eine hohe positive Korrelation von +1 bedeutet, dass bei hohem Aufkommen von x auch ein relatives hohes Aufkommen von y beobachtet werden kann und viceversa. Um auf das klassische Beispiel der Unternehmensplanung einzugehen: Wenn wir die Preise eines Gutes erhöhen, sollte von der Tendenz eine geringere Nachfrage beobachtbar sein und umgekehrt. Und auch wenn wir es oft betont haben: Eine Korrelation sagt für sich genommen nichts darüber aus, ob die Beziehung kausal ist. Zwischen der Geburtenrate und der Anzahl Störche in Städten können Sie eine negative Korrelation über die Zeit beobachten. Daraus können Sie aber nicht schliessen, dass die Störche die Kinder bringen.
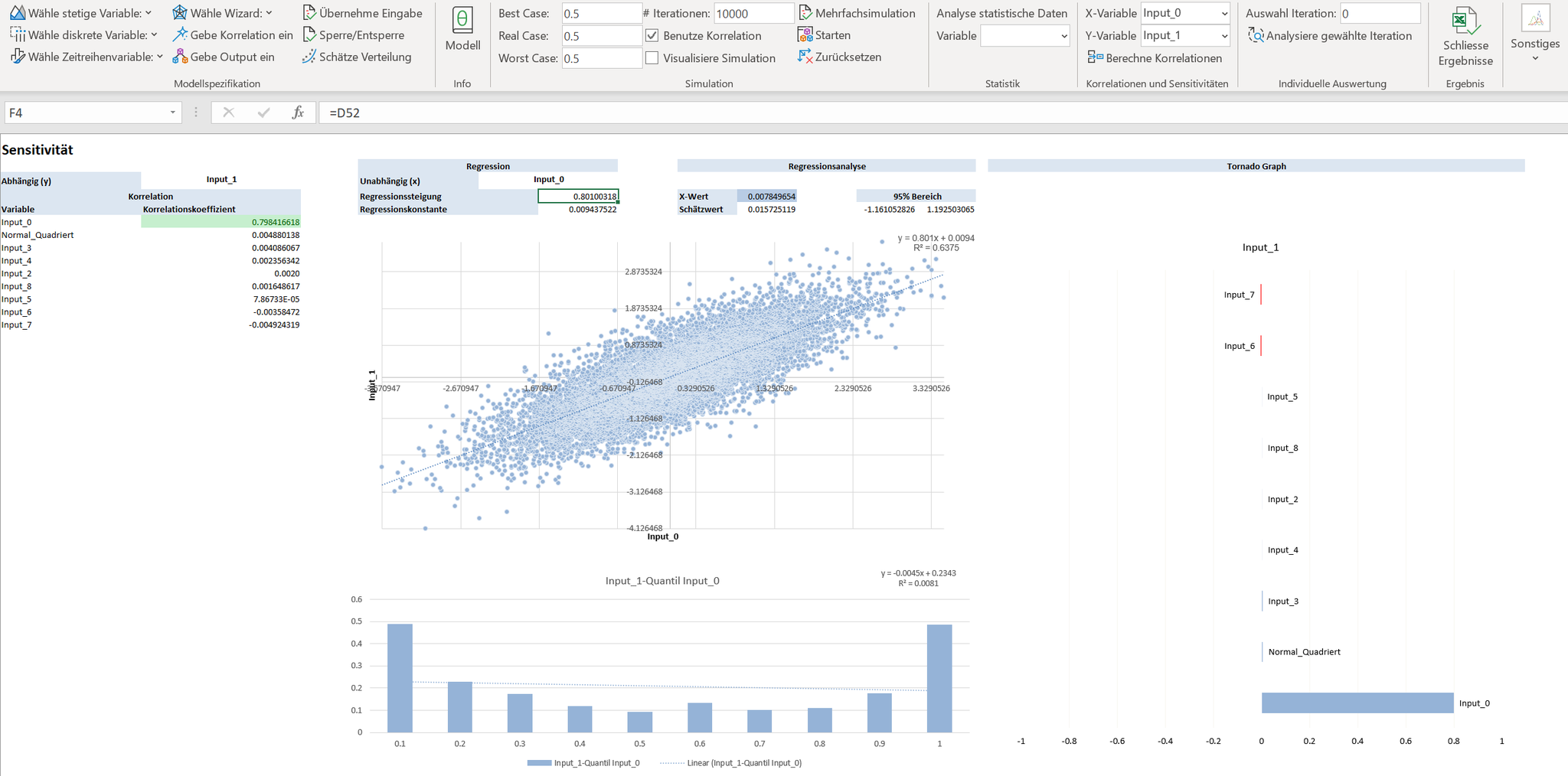
In dem Essay “Thirteen Ways to Look at the Correlation Coefficient” von Joseph Lee Rodgers; W. Alan Nicewander (siehe auch https://www.stat.berkeley.edu/~rabbee/correlation.pdf, aufgerufen im März 2020) werden verschiedene Interpretationen des linearen Korrelationskoeffizienten dargestellt. Wird auf Simulationen abgestützt, eignet sich besonders folgende Darlegung: Hierzu haben wir mit zwei normalverteilte (Input_0, Input_1), zwei gleichverteilte (Input_2 Input_3) und zwei gammaverteilte Zufallsvariablen (Input_4, Input_5) gebildet und diese jeweils mit einem Korrelationskoeffizienten von 0.8 (hergeleitet aus der Gauss-Copula, dazu folgend mehr) miteinander in Beziehung gesetzt. Bilden wir in allen Fällen die Regressionsgerade, also die Linie, bei welcher die Summe der quadrierten Abweichungen der Datenpunkte zur Linie minimiert wird, entspricht der Regressionssteigungskoeffizient - siehe hervorgehobene Zelle - gerade dem Korrelationskoeffizient (die leichten Abweichungen davon sind aufgrund der Simulation zurückzuführen).
Anders sieht der Sachverhalt aus, wenn wir den Korrelationskoeffizienten auf verschiedene Verteilungen, etwa auf eine gleichverteilte (Input_6) und auf eine standardnormalverteilte (Input 7) anwenden. Hier ergeben sich zwei unterschiedliche Steigungskoeffizienten der Regressionsgerade, je nachdem welche Variable auf der x-Achse abgetragen wird.
Werden anschliessend die Verhältnisse der Standardabweichungen beider Zufallsvariablen mit dem Steigungskoeffizienten der Regressionsgerade multipliziert, resultiert wieder der (lineare) Korrelationskoeffizient. Daraus kann folgende Schlussfolgerung entnommen werden: der lineare Korrelationskoeffizient entspricht einer standardisierten Steigung der Regressionsgeraden. Oder einfacher: Falls der lineare Korrelationskoeffizient 0.8 beträgt, dann beträgt die standardisierte Steigung der Regressionsgerade ebenfalls 0.8.
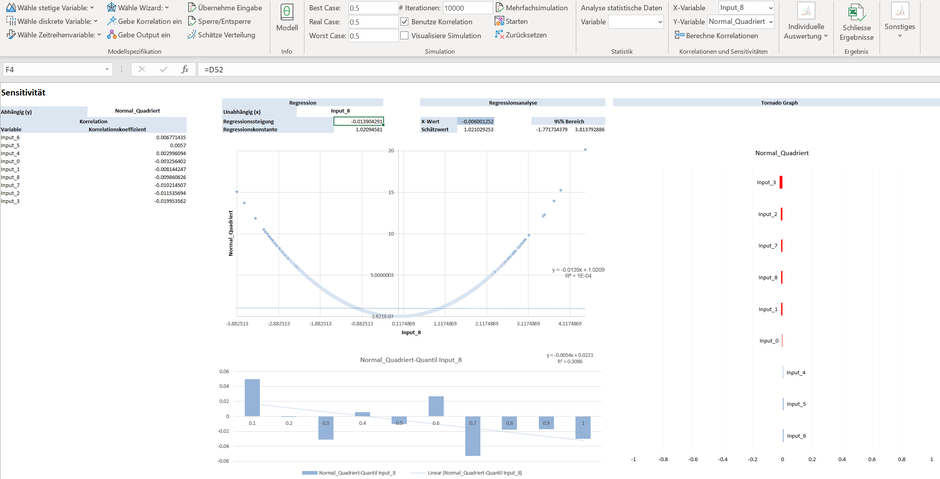
Ungleich komplizierter wird es, wenn die untersuchten Variablen sich gar nicht als lineare Abhängigkeit abbilden lassen, eine Abhängigkeit offenkundig aber besteht. Das klassische Beispiel hierzu ist das Heranziehen der Normalverteilung und deren quadrierten Werte. Der lineare Korrelationskoeffizient ist in diesem Fall praktisch Null (die Abhängigkeit ist eben nicht linear). Aus einem linearen Korrelationskoeffizient von Null kann somit nicht der Schluss gezogen werden, dass keine Abhängigkeit vorliegt.
In den bisher dargestellten Ausführungen haben wir nichts darüber gesagt, wie wir die Datenpaare bei der untersuchten linearen Korrelation gebildet haben, so dass mit dem vorab genannten Korrelationskoeffizient das gewünschte Ergebnis erzeugt wurde. Damit sind wir bei den Copulas. Vereinfacht stellen Copulas eine Beschreibung dar, wie die Datenpunkte beliebiger Verteilungen sich über den gesamten Datenraum erstrecken sollen. Etwa so: «Bei tiefen Werten von x (etwa Preis) und y (etwa Menge) soll die Beziehung sehr stark sein, mit zunehmenden x und y soll diese Beziehung aber abflachen». Eine andere Beschreibung könnte lauten: «Bei tiefen Werten von x und y soll die Beziehung stark sein, mit zunehmenden x und y soll diese Beziehung abschwächen und bei sehr hohen x und y wieder stark zunehmen». Erstere Beschreibung kann auf eine Clayton Copula übertragen werden, letztere auf eine Gauss oder Normal Copula, welche in MC FLO als Standard bei der Korrelationsbildung über den Iman-Conover Ansatz hinterlegt ist (siehe auch diesen Blogbeitrag). Bei beiden Ansätzen – wie unten ersichtlich – resultiert annähernd der vorab definierte Korrelationskoeffizient von 0.8.
Hierbei gilt festzuhalten, dass der Korrelationskoeffizient über alle Datenpaare gebildet wird und folglich eine globale Grösse darstellt. Je nach Beschreibungsmuster (Copulas) können für einzelnen Regionen jedoch unterschiedliche Korrelationskoeffizienten resultieren. Oder mit anderen Worten: Der Korrelationskoeffizient ist nicht notwendigerweise konstant, wie aus den obigen Bildern abgelesen werden kann.
Damit sind wir beim Kern der Finanz- und Bankenkrise (2007/8). Anstatt auf extensive Darstellungen einzugehen, möchten wir folgenden Artikel nahe legen: Catherine Donnelly and Paul Embrechts: "The devil is in the tails: actuarial mathematics and the subprime mortgage crisis" (aufgerufen im März 2020). Aus diesem und dem bisher Dargestelltem lassen sich zwei wesentliche Schlussfolgerungen ziehen:
- Wenn Sie Daten aus einem Bereich beobachten können, schliessen Sie nicht daraus, dass diese Daten unbesehen für einen ähnlichen Sachverhalt als Erklärungsmuster heranzuziehen sind
- Aus einer Korrelationskennzahl kann nichts über die Beziehung im relevanten Bereich ausgesagt werden
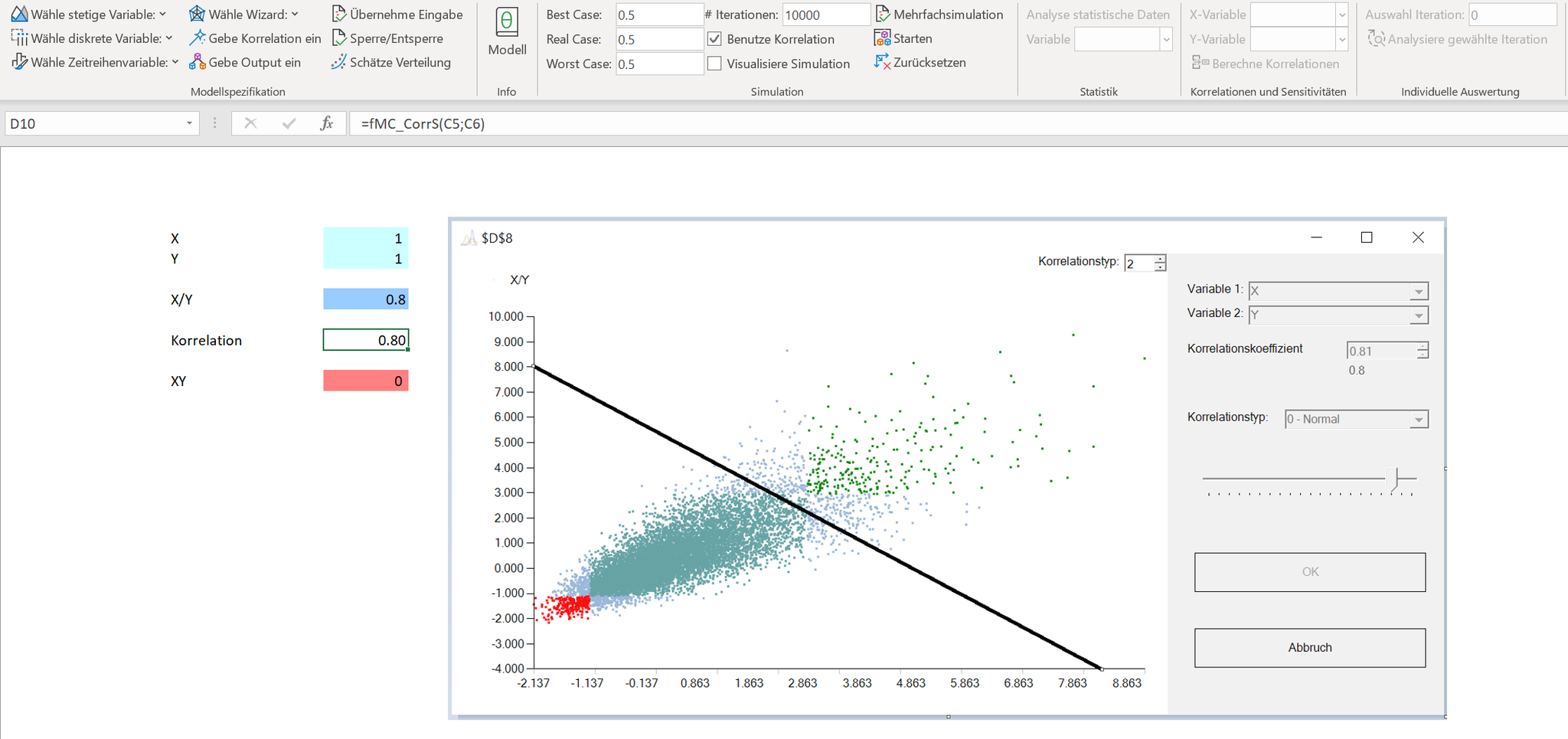
Schauen wir die letzte Aussage vertiefter an. Hierzu haben wir zwei Gumbel-verteilte Zufallsvariablen mit identischer Parametrisierung herangezogen und diese einmal mit einer Gauss Copula und alternativ mit einer Clayton Copula unter Berücksichtigung eines Korrelationskoeffizienten von 0.8 modelliert.
Betrachten wir die Werte rechts von der Diagonalen, welche die Werte von 8 auf beiden Achsen verbindet, wird ersichtlich, dass bei der Gauss -oder Normal Copula (siehe neben "Korrelationstyp") die Werte viel weiter streuen als bei der Clayton Copula. Und das bei gleichem Korrelationskoeffizient und gleichen (Rand-)Verteilungen!
Das ist der Kern der Bankenkrise. In den mathematischen Modellen für die Preisbildung von Collateralized Debt Obligation wurde eine Beziehung im Sinne einer Gauss Copula unterstellt. Vereinfacht ausgedrückt gingen die Modelle davon aus, dass die Zahlungsunfähigkeit von Frau Meier und die von Herrn Schmidt im Krisenfall kaum korreliert. Oder anders: Durch den Beizug der Gauss Copula wurde suggeriert, dass im Krisenfall der Wertverlust eines Portfolios sehr gering ist. Das Ende kennen wir.
Was ist die Essenz? Trotz aller Methoden, welche die Mathematik offenbart, die Modellentscheidung bleibt (noch) beim Menschen. Hinterfragen Sie die Annahmen, seien Sie kritisch. Oder: Wenn Ihnen ein Apfel auf den Kopf fällt, geben Sie nicht Isaac Newton oder Galileo Galilei die Schuld. Denn es gilt: "All models are wrong, but some are useful".
Und: mit Simulationen "sehen" Sie hautnah, was passieren kann - das hilft Überraschungen zu vermeiden.
Epilog - Da MC FLO auch für die Unternehmensplanung eingesetzt wird, knüpft sich folgende Frage an: Was ist zu beachten? Es kommt wie immer auf die Fragestellung an. Vorsicht ist etwa bei der Revisionsplanung geboten: Der Ausfall des Motors und des Getriebes eines Fahrzeuges dürften ab einer hohen Kilometerzahl sehr stark korrelieren, während die Korrelation bei tiefen Laufleistungen eher geringer ausfallen sollte. Eine Datenanalyse hilft hier weiter.
Weitaus wichtiger ist es uns zu betonen, dass Sie Korrelationen als wesentlicher Bestandteil einer zukunftsgerichteten Planung verstehen sollten. Welche funktionalen Abhängigkeiten sind in Zukunft zu erwarten; werden diese positiv oder negativ sein? Dabei reicht es die Korrelationen und die Struktur - um Scheingenauigkeiten zu vermeiden - in einem ersten Schritt grob festzulegen.
Treffen Sie so - auf Basis einer robusteren Planung - bessere Entscheidungen.

















Kommentar schreiben