- Deutsch
- Español
- English
- Blog
- Get it now!
- Shop
- Wiki
- DEU - Stetige Verteilungen
- Gleichverteilung
- Dreiecksverteilung
- Normalverteilung
- LogNormalverteilung
- Betaverteilung
- Gumbelverteilung
- Gammaverteilung
- Exponentialverteilung
- Gekürzte Normalverteilung
- Weibullverteilung
- Pareto-Verteilung
- Cauchy-Verteilung
- ArcSin-Verteilung
- F-Verteilung
- Student-t-Verteilung
- chi2-Verteilung
- PERT-Verteilung
- Fréchet-Verteilung
- Logistische Verteilung
- DEU - Diskrete Verteilungen
- DEU - Zeitreihen
- DEU - Weitere Funktionen
- Referenz
- Umgang mit Variablen
- Interpretation
- Benutzerdefinierte Verteilung
- Begrenzte Verteilungen
- Korrelationen
- Memory Calculation
- Output
- Multiple Simulation / Box-Whisker
- Bayes-Faktor
- Forecast-Tool
- Batch-Funktion
- Datenanpassung
- Benford Analyse
- Dos and don'ts
- Bootstrap
- Decision Information Package
- Spider Diagramm
- Naive Bayes Klassifikation
- Risikomatrix
- DEU - Stetige Verteilungen
MC FLO leicht gemacht - Beispiele
Hier sehen Sie an den mit MC FLO mitgelieferten Beispielen das breite Einsatzspektrum von MC FLO. Weitere Beispiele und die entsprechenden Excels finden Sie in unserem Blog.
MEMORY CALCULATION ENGINE
Mit der Memory Calculation Engine werden die Berechnungen bereits mit Aufrufen der Arbeitsmappe gestartet. Dies erlaubt eine höchste Automatisierung.
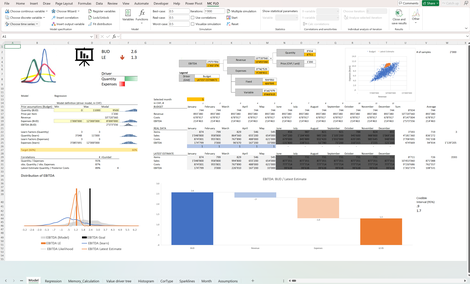
Latest Estimate: Die Planung und Steuerung der finanziellen Kenngrösse EBITDA wird anhand von generativen Verfahren unter Einschluss der Unsicherheit aufgezeigt.
a) Ausgangslage bilden unsichere Annahmen zu Verkaufsmengen, Aufwand etc.
b) diese werden aggregiert, womit sich eine Verteilung des möglichen EBITDA ergibt (Prognose, Forecast)
c) aus der Prognose wird ein Ziel abgeleitet, etwa der EBITDA Wert am 60%-Perzentil
d) anhand der gemessenen Daten wird die Prognose verfeinert und ggfs. das Ziel angepasst
Ersichtlich ist in allen Phasen, welche Treiber massgeblich das Ergebnis beeinflussen und somit prioritär zu steuern sind.

Budgetplanung: Weiterführendes Beispiel, wie Forecast, Planung und Zielwertsetzung mit generativen Verfahren umgesetzt werden.
Generative Verfahren, welche die Unsicherheit explizit bei der Treibermodellierung berücksichtigen, sind hoch flexibel, hier anhand des Einbezugs von Korrelationen ersichtlich.
Untersuchungsobjekt ist die Aufwandsplanung für den Maschinenpark eines Unternehmens. Die Planung soll konservativ, robust und somit mit einer geringen Ambition von 10% auf alle möglichen Werte erfolgen. Unter Einschluss aller möglichen - zum Zeitpunkt der Entscheidung - un vorliegenden Informationen sollte der Aufwand mit 111 MCHF budgetiert werden.
Nach Beobachtung von effektiven Daten - welche deutlich unter den ursprünglichen Annahmen liegen - kann bei Einhaltung der 10%-Ambition der Budgetkurs auf ca. 89 MCHF angepasst werden.
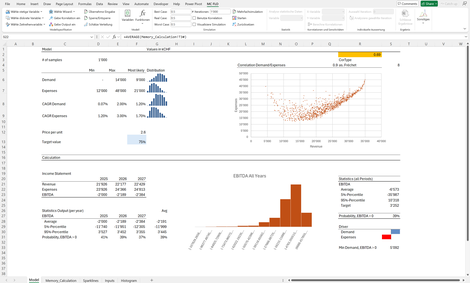
Planung: Drittes Beispiel, welches den Wert generativer Verfahren bei der Planung aufzeigt.
Die Planung umfasst drei Jahre, welche sowohl aggregiert (alle Jahre) als auch einzeln erfasst ist. Aufgrund der Jensenschen Ungleichung wird ersichtlich, dass die 95% Perzentil der Planung über drei Jahre nicht dem Durchschnitt des 95% Perzentils jedes einzelnen Jahres entspricht. Allgemein wird dies auch als Diversifikationseffekt bezeichnet.
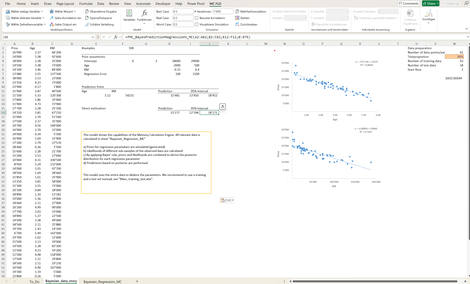
Multiple (bayessche) lineare Regression: Führt eine multiple lineare Regression durch.
Ausgangslage: Es soll der Preis von gebrauchten KFZ anhand der Treiber KM und Alter (Age) bestimmt werden.
Da kein "Vorwissen" im Sinne eines Priors vorgegeben ist, wird anhand einer kleinen Stichprobe eine Initialisierung der Regressionsparameter vorgenommen und anschliessend die Posteriorverteilung anhand des gesamten Datensatzes bestimmt.
Es wird eine Prognose samt Prognoseintervall ausgegeben. Alternativ wird direkt eine Prognose erstellt.
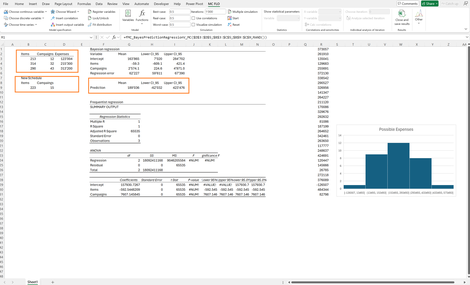
Regression short: Die Bayessche Regression liefert selbst dann Daten und Prognosen, wenn die Datenlage sehr dünn und mit der klassischen Statistik verlässliche Lösung möglich ist.
Im Folgenden haben wir ein Modell mit zwei erklärenden Variablen (Items, Campaigns) und drei beobachteten Datensätzen. Falls im nächsten Monat 223 Items abgesetzt und 15 Compaigns lanciert werden sollen, welcher Umsatz ist im Erwartungswert und unter Einschluss des 95%-glaubhaften Intervalls zu erwarten?
Während die klassische Statistik in Bezug auf die Regressionsparameter keine Unsicherheit (die 95% Konfidenzintervalle sind gleich) zu erfassen vermag. zeichnet die Bayessche Regression ein erklärbares Bild.
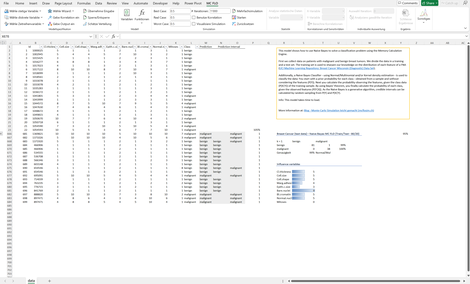
Klassifikation: Auf der Bayesschen Statistik fussender Algorithmus zur Identifikation der Klassenzugehörigkeit ("Klassifizierung") von Beobachtungen, hier anhand von Daten zur Brustkrebsdiagnose.
Dargestellt werden die Trefferquote, der Vertrauensbereich einer konkreten Prognose und die Einflussvariablen einer Prognose.
Bayessche Statistik - Lernen AUS DATEN
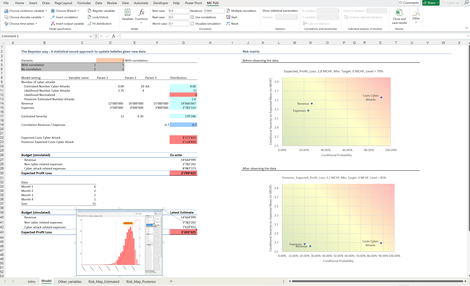
Bayes Risk Matrix: Zeigt anhand einer kombinierten Umsatzplanung unter Einschluss eines klassischen Risikoregisters für Cyberattacken auf, wie konsistente Entscheidungsgrundlagen mit einer quantitativen - auf Basis der Bayesschen Statistik basierenden - Risikomatrix aufbereitet werden.
Vor Beobachtung von Daten haben Cyberattacken den grössten Einfluss (Steuerungshebel) auf den Gewinn, diese können die Zielvorgabe von O CHF nach unten durchbrechen (daher die Einordnung im roten Bereich).
Mit Beobachtung von Cyberattacken und deren Auswirkungen wird mit der Formel von Bayes der Sachverhalt neu bestimmt. Es zeigt sich, dass die Zielvorgabe von 0 CHF eingehalten werden kann. Den grössten Einfluss auf die Zielvorgabe haben weiterhin die Cyberattacken, aber sie gefährden aktuell die Zielerreichung nicht akut. Daher die Abstufung dieser Treibervariable auf den hellroten Bereich.

Bayes_A_B_Test : Prüft eine Gruppe (Variation) gegenüber einer Kontrollgruppe auf Unterschiede.
Als Beispiel wird ein Test untersucht, bei der Probanden eine neue Homepage und eine alte Homepage vorfinden. Anhand der Anzahl Verkäufe soll herausgefunden werden, ob die neue Homepage (Variation) besser bei der Kundschaft ankommt oder nicht.
Mit einem Bayesschen A/B Test kommt die untersuchende Person zur Überzeugung, dass die Variation besser ist. Eine vollständige Überzeugung liegt anhand der gemessenen Daten jedoch nicht vor.

Bayes_Cyber_Attacks: Stellt anhand des Vorwissens und gemessenen Daten zu Cyberattacken eine Aussage zu zukünftigen Cyberattacken.
Das Vorwissen wird - bei Fehlen von Daten - anhand von (subjektiven) Einschätzungen und einer zugehörigen Wahrscheinlichkeitsverteilung beschrieben. Sobald Daten vorliegen, kann dieses mit dem Vorwissen anhand des Satzes von Bayes zu einer Posteriorverteilung überführt werden, Die Posteriorverteilung gibt Auskunft über die zukünftigen unsicheren Cyberattacken innerhalb einer Zeitspanne wieder.
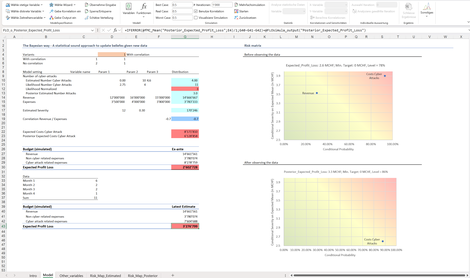
Bayes_CyberAttacks_1: Erweitert das in Cyber_Attacks beschriebene Problem um Zielvorgaben. Dabei werden die Auswirkungen der Einflussgrössen auf die Zielerreichung mit einer Risiko-Matrix dargestellt. Hierbei werden zwei disjunkte Szenarien anhand der Mehrfachsimulation analysiert
Das erste Szenario ignoriert mögliche Zusammenhänge (Korrelationen) zwischen den Einflussgrössen. Beim zweiten wird ein Zusammenhang einer Fréchet Copula berücksichtigt.
Sowohl vor als nach Beobachtung von Daten kann der Einfluss der Treibervariablen auf das Ergebnis anhand einer Risiko-Matrix dargestellt werden. Während vor Beobachtung die Cyber-Attacken als wesentlicher Treiber des Ergebnis klassifiziert werden können, kann nach Beobachtung eine Entwarnung ausgesprochen werden.
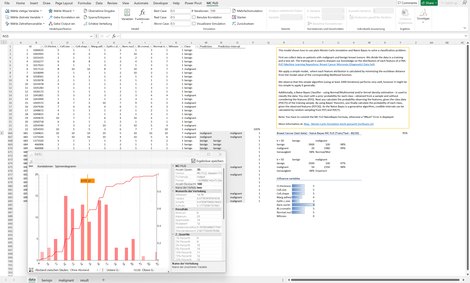
Naive Bayes: Auf der Bayesschen Statistik fussender Algorithmus zur Identifikation der Klassenzugehörigkeit ("Klassifizierung") von Beobachtungen, hier anhand von Daten zur Brustkrebsdiagnose.
Dargestellt werden die Trefferquote, der Vertrauensbereich einer konkreten Prognose und die Einflussvariablen einer Prognose.
Zum Nachvollzug wird anhand eines Simulationsergebnisses der Berechnungsweg vorgestellt.
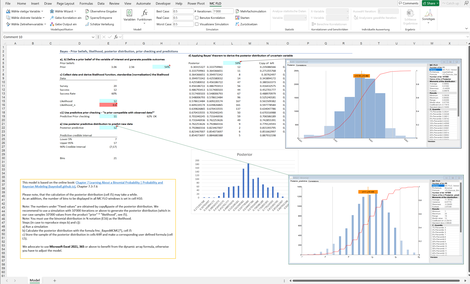
Bayes_I: Zeigt anhand der Bayessschen Statistik auf, wie "Lernen aus Daten" algorithmisch umgesetzt wird.
Ausgangspunkt ist ein Vorwissen - hier über die Zustimmung von Personen zu einer beliebigen Fragestellung. Annahme ist, dass 54% der Personen zustimmen. Die Zustimmungsrate gilt aber als unsicher. Diese kann zwischen ca. 17% und 87% variieren.
Bei einer Umfrage von 20 Teilnehmern befürworten 12 das Vorhaben. Das Umfrageergebnis kann als Resultat einer Binomialveteilung aufgefasst werden.
Durch Kombination von Vorwissen und Umfrageresultat kann das Wissen über die echte Zustimmungsquote geschärft und dessen Unsicherheit reduziert werden.
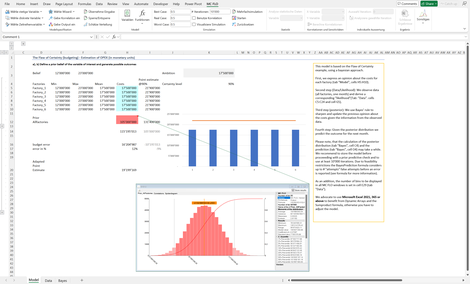
Bayes_II: Zeigt anhand der Fabrikplanung auf, wie der Bayessche Ansatz beim Zusammenspiel zwischen Prognose und Planung funktioniert.
Ausgangslage sind unsichere Grössen, wie mögliche Fabrikkosten pro Jahr. Diese werden anhand einer Gleichverteilung mittels Monte-Carlo Simulation aggregiert. Die Aggregation stellt den Prognoseraum dar. Aus diesem wird ein Zielwert abgeleitet.
Nach Messung von konkreten Kosten der Fabriken kann die Prognose geschärft, mit den Zielwerten gegenübergestellt und mögliche Handlungsempfehlungen abgeleitet werden.
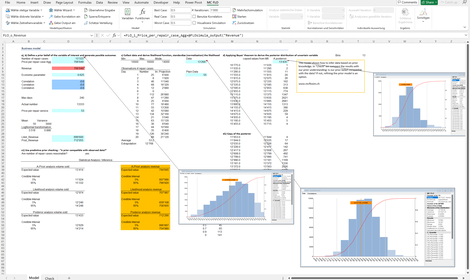
Bayes_III: Erneutes Beispiel zur Illustration von "Lernen aus Daten". Unsicheres Vorwissen wird mit gemessenen Daten anhand des Satzes von Bayes in ein angepasstes Wissen (Posterior) überführt. Dies als Wahrscheinlichkeitsverteilung vorliegende angepasste Wissen wird als Prognoseinstrument eingesetzt.
Unabhängig davon, kann das Verständnis des unsicheren Vorwissens - etwa abgeleitet aus Treibermodellen - mit den Daten verprobt werden. Liegen die Daten ausserhalb der Bandbreite des Vorwissens, entsteht kein Lerneffekt. Das Vorwissen kann nicht von den Daten profitieren. Umgekehrt bedeutet es, dass das Vorwissen nicht mit den Daten kompatibel ist. Es läge dann eine Missspezifikation vor. In diesem Beispiel sind die Daten mit dem Vorwissen kompatible und der Lerneffekt tritt ein.
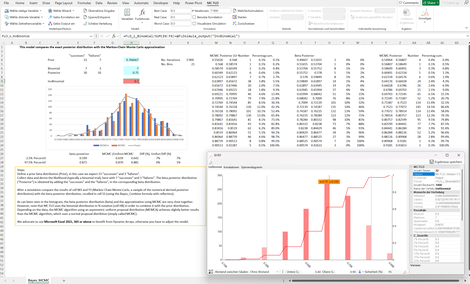
Bayes_Simple_Beta: Die Kombination von Vorwissen und gemessenen Daten zum "Posteriorwissen" anhand des Theorems von Bayes kann nur bei einfachen Wahrscheinlichkeitsverteilungen analytisch gelöst werden. Für alle anderen Verteilungen und möglichen daten-generierenden Prozessen sind Näherungsverfahren notwendig. MC FLO wendet den bekanntesten Algorithmus - Markov Chain Monte Carlo (MCMC) - an, welcher Stichproben aus der Posteriorverteilung zieht. Anhand des Beispiels wird ein exaktes Verfahren mit MCMC verglichen.
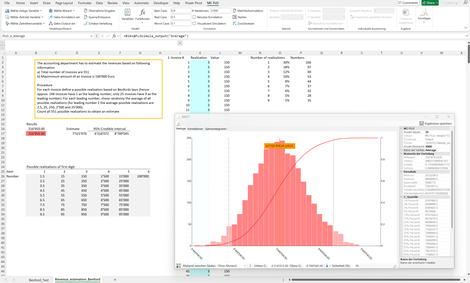
Benford_I: Anhand der Benford Verteilung wird aufgezeigt, ob Daten manipuliert wurden oder nicht. Hierbei auf den Bayes-Faktor abgestützt. Zusätzlich wird ein klassischer t-Test angewandt. Während der t-Test eine Manipulation der Daten für glaubwürdig hält, ist bei Anwendung des Bayes-Faktors keine Manipulation ersichtlich. Klingt paradox, ist es aber nicht. Leider wird bei der klassischen Statistik oft übersehen, dass der Verwerfungsbereich mit der Anzahl Stichproben korreliert. Je grösser die Anzahl Stichprobe ist, desto kleiner sollte das Signifikanzniveau sein.
Zusätzlich wird anhand weniger Informationen, hier der Anzahl Rechnungen und des maximalen Rechnungsbetrages, der Umsatz geschätzt.
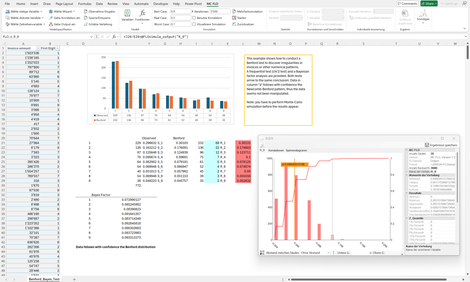
Benford_II: Anhand von 772 Rechnungen wird analysiert, ob die Daten einer Benford-Verteilung folgen.
Für die Prüfung wird der Bayes-Faktor angewandt. Dieser prüft die Nullhypothese - abgeleitet aus der Benford Verteilung - gegenüber allen anderen Hypothesen.
Bei 772 Rechnungen sollte die Zahl 9 als führende erste Zahl des Rechnungsbetrags ca. 35 mal vorkommen (4,5%), gemessen wurden aber 38 Vorkommnisse (4,9%). Zur Prüfung, ob die Abweichung von 0,4%-Punkten durch den Stichprobenumfang begründet werden kann, wird eine Beta-Binomialverteilung als Testverteilung herangezogen. Bei allen Zahlen ist eine Abweichung von der Benford-Verteilung nicht begründet.
Bayessche LiNEARE Regression
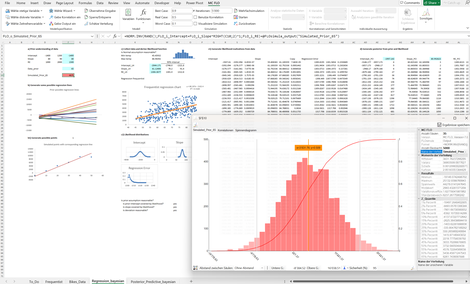
Bikes Training Test: Die Regressionsparameter (etwa Schnittpunkt, Steigung) werden initial anhand von Expertenwissen oder Treibermodellen bestimmt. Die Treibermodelle geben mögliche Werte, welche zukünftig auftreten werden, vor. Diese stellen somit Prognosen dar.
Mit Aufkommen von Daten wird die Likelihood bestimmt: die Übereinstimmung der Daten bei gegebenem Regressionsparameter.
Durch Anwendung des Satzes von Bayes wird abschliessend die Wahrscheinlichkeit der initial angenommenen Regressionsparameter mit den gemessenen Daten ermittelt, womit neue Prognosen erstellt werden. Es werden glaubhafte Intervalle und verschiedene Modelle dargestellt. Zudem werden die Daten in eine Trainings -und Testmenge unterteilt. Das Beispiel untersucht den Zusammenhang zwischen Fahrradfahrten und der Temperatur.

Bayesian Multiple linear Regression: Anhand einer multiplen, linearen Regression wird der Bayessche generative Ansatz vertieft. Konkret soll der Preis von Gebrauchtwagen bestimmt werden. Dabei wird unterstellt, dass der Preis von den zurückgelegten KM und dem Alter (linear) abhängt.
Mit einem Vorwissen über die Regressionsparameter (Achsenabschnitt, KM, Alter) wird eine Prognose vor Beobachtung der Daten erstellt.
Nach Beobachtung der Daten wird die Prognose und damit der Zusammenhang anhand des Satzes von Bayes neu beurteilt. Einige Kennzahlen werden zusätzlich aufbereitet, um das beste Modell (einfache, multiples Modell) auszuwählen.
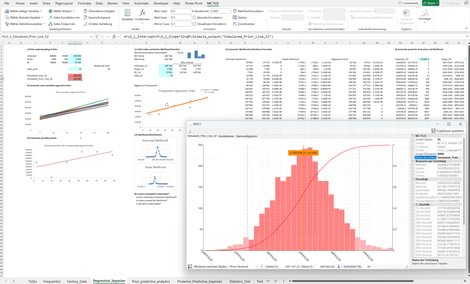
Factory Regression: Anhand einer einfachen, linearen Regression werden generative Verfahren als Treibermodelle vorgestellt. Idee: Es soll der Aufwand einer Maschine gemessenen werden, wobei der Schnittpunkt der Regression dem fixen Aufwand und die Steigung dem variablen Aufwand entspricht. Mittels Simulation werden a-priori Werte, somit Prognosen, vor Messung der Daten erstellt.
Mit Vorliegen von echten Daten wird das Verständnis über die Regressionsparameter (etwa Schnittpunkt und Steigung) neu geschärft. Siehe auch: Bayessche lineare Regression - Auf zu neuen Ufern! - Monte-Carlo Simulation leicht gemacht
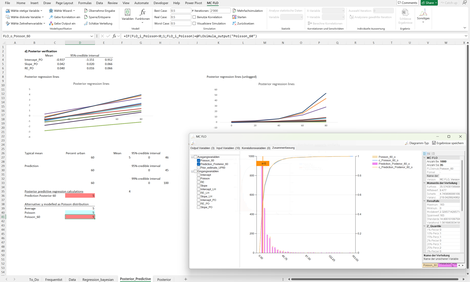
Poisson Regression: Führt eine lineare Regression mit Annahme Poisson verteilter Ausgangsgrössen durch.
Es soll der Zusammenhang zwischen städtischer Bevölkerungsdichte (Eingangsvariable) und der Anzahl LGBTQ freundlicher Gesetze in den USA (Ausgangsvariable) untersucht werden. Im Gegensatz zu einer klassischen Regression ist die Ausgangsgrösse als ganze Zahl zu bestimmen, womit eine Poisson-verteilte Regression herangezogen wird.
Analog der bisherigen Beispiele wird Schritt-für-Schritt die Herleitung der Regressionsparameter gemäss dem Satz von Bayes aufgezeigt.
Klassische Probleme und Lösungen

Birthday_problem: Klassisches Beispiel, welches aufzeigt, wie fehlerhaft der Mensch mit Wahrscheinlichkeiten umgeht.
Das Geburtstagsproblem legt dar, wie Übereinstimmungen öfters vorkommen, als vorher angenommen.
Hier: Wie hoch ist die Wahrscheinlichkeit, dass auf dem Fussballfeld (11 Spieler, 1 Schiedsrichter) zwei Personen am gleichen Tag Geburtstag haben?
Die meisten Menschen würden die Anzahl Personen durch die Anzahl Tage eines Jahres dividieren, um auf die gesuchte Grösse zu schliessen (23 / 365 = 13%), Mit einer Simulation können Sie den Sachverhalt spielerisch nachvollziehen. Lassen Sie sich überraschen.
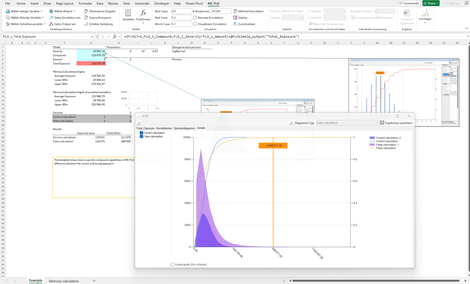
Compound_Function: Zeigt auf, wie unsichere Grössen -etwa Merkmalsverteilungen - korrekt multipliziert werden müssen. Dieser Vorgang wird auch als "Faltung" bezeichnet.
Leider werden fälschlicherweise beide Grössen multipliziert und das Resultat davon in die Ergebnisverteilung übernommen. Korrekt ist aber aus der Anteilsgrösse (Anzahl Fälle) ein fixer Wert n aus der zugehörigen Merkmalsverteilung zu nehmen und n mal eine Zufallszahl aus der anderen Merkmalsverteilung zu ziehen und diese zu addieren.
Beide Verfahren führen zu unterschiedlichen Verteilungen, auch wenn die Erwartungswerte in beiden Fällen gleich sind. Zur Differenzierung wird auf die Mehrfachsimulation zurückgegriffen. Ergänzend wird das richtige Vorgehen auch mit der ultra-schnellen Memory Calculation Engine vorgestellt.
Flower: Zeigt die Mächtigkeit generativer Modelle, hier am Beispiel der Generierung einer Blume anhand des Abbild einer "echten" Blume.
Just for fun!
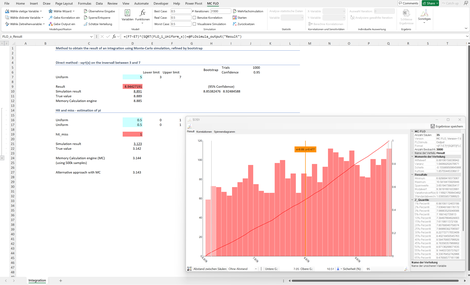
Integration: Zeigt spielerisch auf, wie die Integration und die Bestimmung der Zahl Pi mittels Simulation gelöst wird - ohne Formeln. So sollte Schule sein!
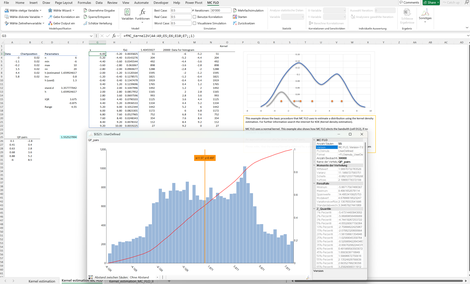
Kernel_estimation: Moderne Algorithmen - insbesondere im Machine Learning Bereich - machen von der Kerndichteschätzung Anwendung. Sie ist hat zum Ziel den "datengenerierenden Prozess" anhand der effektiv gemessenen Daten zu schätzen. Im Gegensatz zur klassischen Verteilungsanpassung ist der Kerndichteschätzer parameterlos und auch für eine geringe Anzahl Daten flexibel anwendbar.
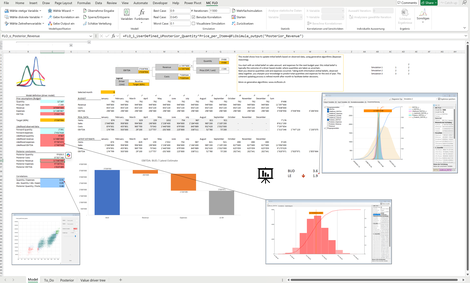
Latest Estimate: Zeigt auf, wie anhand von Daten ein Lernprozess stattfindet. Ausgangslage sind Annahmen über die Zielvariable (etwa EBITDA), welcher sich aus den unsicheren Annahmen zu Umsätzen, Aufwand und möglichen Korrelationen zusammensetzt. Das Ergebnis hiervon aus einer Monte-Carlo Simulation entspricht dem Vorwissen (Prior).
Nach Beobachtung von Daten (Likelihood) wird dieses Wissen durch Anwendung des Satzes von Bayes geschärft (Posterior).
Das Beispiel zeigt auf, wie moderne generative Verfahren zur Prognose angewandt wird. Einen alternativen Ansatz zur Bestimmung der Absatzmenge finden Sie zusätzlich hier.
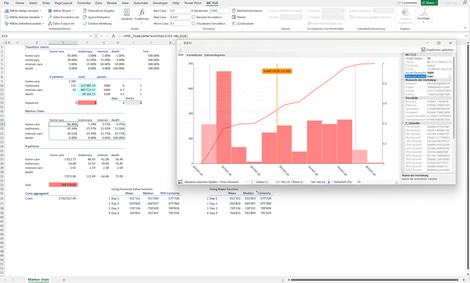
Markov Chain: Markov Chains stellen Übergange zwischen verschiedene Zustände mit Wahrscheinlichkeiten dar.
In diesem Fall sollen die Aufwände der nächsten Tage eines Spitals anhand der Anzahl Patienten und deren Gesundheitszustandes ermittelt werden.
Mit Markov Chains verschiedene Übergänge simuliert und somit mögliche Aufwände transparent aufgezeigt.
Das Spital kann auf dieser Basis die Personaleinsatzplanung und die Liquidität optimieren
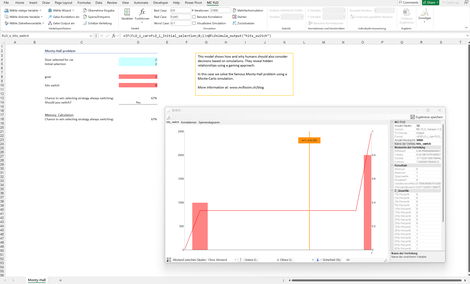
Monty Hall: Paradebeispiel zur Illustration, wie Menschen Wahrscheinlichkeiten falsch einschätzen, hier am Beispiel des "Ziegenproblems".
Das Beispiel kann mit der klassischen Monte-Carlo Simulation und mit Memory Calculation Engine von MC FLO nachvollzogen werden.
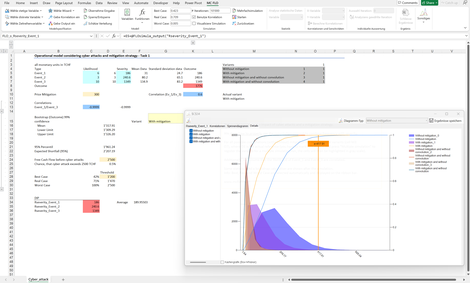
OpRisk: Zeigt anhand der Mehrfachsimulation auf, warum Beziehungen (Korrelationen) und das Faltungsprinzip zwischen Variablen bei der Modelllierung von Unsicherheit tragend sind.
Korrelation: Wahrscheinlichkeitsorientierte Beschreibung des Zusammenhangs zwischen Variablen
Faltung: Berechnungsschema bei der Multiplikation zweier unsicherer Variablen
In diesem Beispiel soll anhand von Cyber-Attacken eine Mitigationsstrategie diskutiert werden. Ist es wirtschaftlich sinnvoll, sich gegen Cyber-Attacken zu versichern oder nicht?
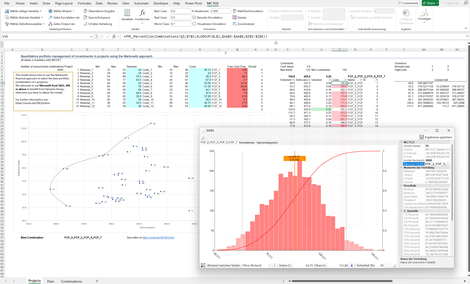
Portfolio Markowitz: Es sollen n Projekte mit unsicheren Ergebnissen in Bezug auf Wirkung und Aufwand (Kosten) so zusammengestellt werden, dass der Ertrag bei gleichzeitiger Minimierung der Volatilität maximiert wird. Dies unter Berücksichtigung, dass gewisse Projekte durchgeführt und "Guardrails" hinsichtlich der Investitionssumme eingehalten werden. Zudem sind Korrelationen abzubilden.
Das ist die Sternstunde der Portfoliotheorie von Markowitz, welche anhand von Simulationen hautnah und praxisrelevant umgesetzt wird.

Quantile Probability: Wie kann eine Verteilung ohne Formeln anschaulich definiert und simuliert werden?
Genau hier setzen wir mit dem Quantile Probability Pairs Ansatz an: Sie definieren Paare (Perzentile, Werte) und geben Minimum und Maximum an. Mit einer benutzerdefinierten Verteilung können Sie dies sofort in die Simulation integrieren.
Im Beispiel ist festgehalten, dass die unteren 10% aller möglichen Ergebnisse den maximalen Wert 21 annehmen, die unteren 95% den Wert von 120.

Real Options: Zeigt anhand der Real-Optionen Theorie und Monte-Carlo Simulation auf, warum gestaffelte Entscheidungen unter Unsicherheit gewinnmaximierend sein können.
Idee: Ein Markt soll mit einem neuen Produkt bedient werden, doch aufgrund von Unsicherheit ist der Markterfolg nicht garantiert. Im Rahmen einer statischen Investitionsrechnung kann mitunter ein negativer Cash-Flow in Bezug auf den Bewertungszeitpunkt resultieren. Durch gestaffelte Investitionen resultiert hingegen ein positiver Cash-Flow (Barwert), dies weil im Zeitablauf die Marktnachfrage offenbart wird und im Zweifel die Investitionen gering sind, bei positiver Annahme im Markt die Gewinnchancen sich aber erhöht haben.
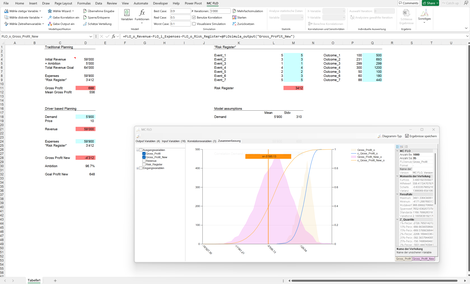
RIsk Register: Die traditionelle Planung ist einer Punktplanung, welche um unsichere Ereignisse anhand eines Risikoregister ergänzt wird.
Wir zeigen auf, dass Mehrwert und bessere Entscheidungen durch Kombinationen beider Welten unter Einschluss der Unsicherheit erzeugt wird.
Sowohl die traditionelle Planung als auch das Risikoregister sind als Ereignisse unter Unsicherheit aufzufassen. Weder die Absatzmenge noch mögliche andere auf den Gewinn Einfluss nehmende Ereignisse sind "sicher". Unsichere Ereignisse sind mit Wahrscheinlichkeiten zu hinterlegen. Diese können rein subjektiv formuliert sein. Mit einer Simulation schaffen Sie Transparenz - ihre Entscheidungen werden bewusster. Info: Das Modell bildet Abhängigkeiten zwischen Variablen als
Korrelation ab.
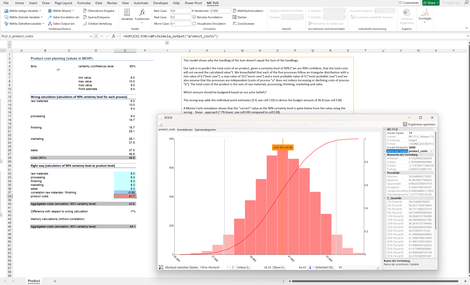
Sandbagging: "Die Summe der Sandsäcke entspricht nicht dem Sandsack der Summe". Was erst einmal widersprüchlich klingt, kann anhand einer Simulation bewiesen werden.
Viele Planungen laufen gemäss einem bekannten Muster ab: Für verschiedene Positionen werden Planwerte unter Einschluss von Ambitionen erstellt und diese aggregiert. Die Summe der Planwerte wird als Ambition festgelegt.
Mittels Simulation kann jedoch aufgezeigt werden, dass die Ambition in der Aggregation nicht der Summe der einzelnen Positionen entspricht. So lässt sich erklären, warum Budgets per Ende Jahr nicht ausgeschöpft oder Zielvorgaben - trotz exakter Umsetzung nach Plan - nicht eingehalten werden. Anders ausgedrückt: Wenn Sie unsichere Positionen addieren, dürfen Sie sich nicht auf die klassische Schulmathematik verlassen!
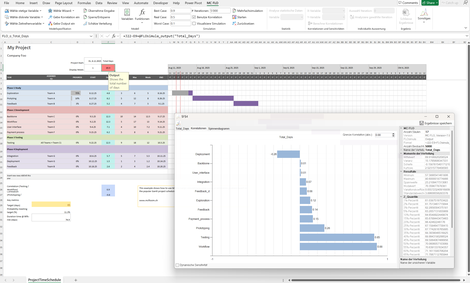
GANTT: Warum Projekte nicht ihre Zeitvorgabe halten, wird im folgenden GANTT Diagramm und anhand einer Simulation ersichtlich.
Dargestellt sind verschiedene Aktivitäten (Tasks), deren Zeitdauer und Abhängigkeiten zwischen den Aktivitäten.
Ziel ist, dass das Projekt in 65 Tagen abschlossen sein soll. Anhand einer Simulation kann gezeigt werden, dass in nur von 11 von 100 Fällen dieses Ziel unterschritten wird.
Wird von einer geringen Ambition ausgegangen - in einem solchen Fall soll das Projekt in 90 von 100 Fällen gemäss oder unter der Zielvorgabe abgeschlossen sein, ist eine Zeitdauer von ca. 75 Tagen als Ziel vorzugeben.
Soll trotzdem am Ziel von 65 Tagen festgehalten werden, ist anhand einer Tornado-Analyse ersichtlich, dass die Aktivitäten "Workflow" und "Testing" prioritär gesteuert werden sollten.

Subject Matter Experts: Als "Wisdom of Crowds" oder auch die "Weisheit der Vielen" beschreibt das empirisch bestätigte Phänomen, wonach (unabhängige) verschiedene Prognosen in einer Gruppe besser abschneiden als die Lösungen einzelner Teilnehmer (The Wisdom of Crowds. Why the Many Are Smarter than the Few and How Collective Wisdom Shapes Business, Economies, Societies and Nations, James Surowiecki).
In diesem Beispiel wird dargestellt, wie wir diesen Ansatz in der Praxis pflegen. Für die Umsatzprognose werden vier Experten (Peter, Jane,...) zu ihren Vorstellungen unabhängig befragt. Jeder Teilnehmer gibt die Angaben unter Unsicherheit an. Peter geht davon aus, dass der Umsatz mindestens 11 MCHF, maximal 17 MCHF und im wahrscheinlichsten Fall ca. 13 MCHF beträgt. Die unterschiedlichen Meinungen werden aggregiert und anhand der bisherigen Prognosegüte der einzelnen Teilnehmer gewichtet. Für das 75%-Perzentil beträgt die Umsatzprognose ca. 13.3 MCHF, im Median (50% Chance, dass der effektive Umsatz grösser oder kleiner ist), liegt der Umsatz bei ca. 12.1 MCHF.
Eine robuste Prognose aber auch Zielwertsetzung kann mit diesem Verfahren rasch umgesetzt werden.
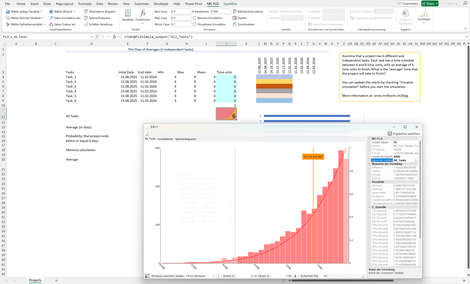
Flaw of Averages: Aus "The Flaw of Averages" von Sam Savage oder warum einzelne Durchschnittswerte nicht für eine Entscheidung taugen.
Der Sachverhalt: Sie haben n verschiedene, unabhängige Aktivitäten (Tasks) mit unsicheren Prozesszeiten, welche zwischen 4 und 8 Tage schwanken und im Durchschnitt eine Prozesszeit von 6 Tagen aufweisen. Alle Aktivitäten werden zeitgleich gestartet. Nach wie vielen Tagen werden alle Aktivitäten im Durchschnitt beendet sein?
Die meisten Menschen würden 6 Tage nennen. Das ist aber falsch. Es sind ca. 7.43 Tage! Mit einer Simulation können Sie der Ursache auf den Grund gehen. Wir hoffen, dass Sie spätestens jetzt von der Monte-Carlo Simulation überzeugt sind.
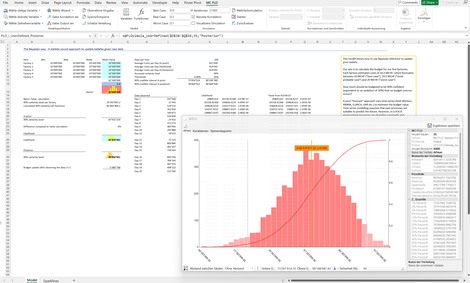
Flaw of Multiplication: Wie können Prognosen erstellt, aus diesen Zielwerte abgeleitet und anhand beobachteter Daten der gesamte Planungsprozess optimiert werden?
Unsere Antwort darauf sind generative Verfahren - keine LLM - aber Treibermodelle, welche anhand von Monte-Carlo Simulationen tausende von realistischen Szenarien generieren und somit einen Prognoseraum erzeugen, aus dem Ziele abgeleitet werden.
Treibermodelle müssen sich jedoch an echten Daten messen können. Hier bieten generative Verfahren, welche auf der Bayesschen Statistik aufsetzen, Mehrwert. Hier anhand einer Budgetplanung eines Fabrikparks dargestellt.
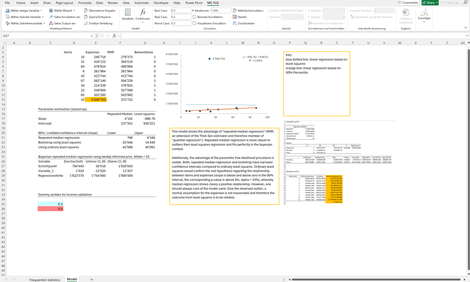
Median regression: Falls "Ausreisser" in der Stichprobe vermutet werden, kann das Konzept der Medianregression zum Tragen kommen. Im Gegensatz zu der klassischen Regression, bei der die "Kleinste-Quadrate" Methode zur Anwendung kommt, wird bei der Median Regression die absolute Abweichung zwischen den beobachteten und geschätzten Werten minimiert.
Im Folgenden wird der Zusammenhang zwischen produzierten Einheiten und Aufwand untersucht. Aufgrund eines "Ausreissers" kommt die Kleinste-Quadrate Methode zum Schluss, dass kein "statistischer Zusammenhang" zwischen beiden Grössen besteht. Mit Anwendung der Median Regression kann hingegen ein positiver Zusammenhang nicht verneint werden.
Folgend sehen Sie hier, wie Sie die Investitionsbedarfsplanung mit Predictive Analytics bestimmen können. Das Muster können Sie für beliebige Bedarfsplanungen einsetzen.
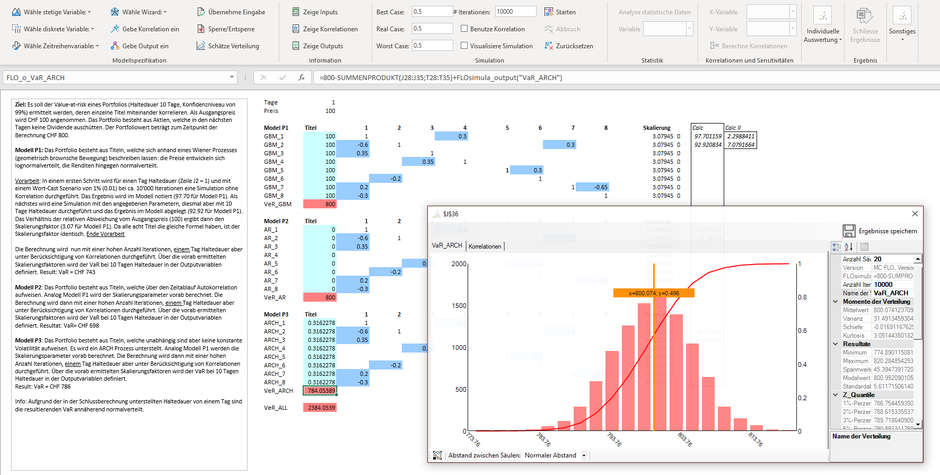
Hier zeigen wir Ihnen, wie Sie den Value-at-Risk bei Zeitreihenprozessen und unter Berücksichtigung von Korrelationen mit MC FLO ermitteln können. Sehen Sie hierzu unseren Blogbeitrag.
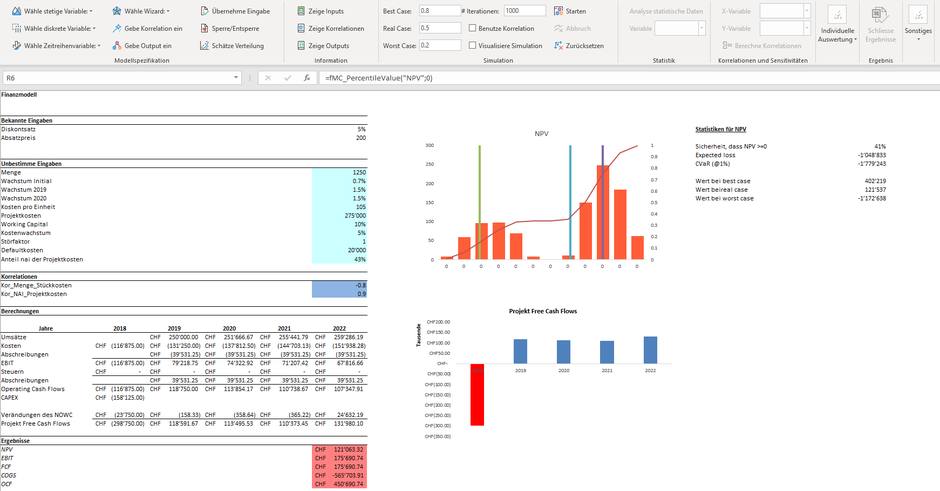
Folgend das mit MC FLO mitgelieferte Beispielprogramm einer Investitionsentscheidung, mit detaillierteren Angaben zum diskontierten Geldfluss (net present value - NPV), alles direkt in der Modellarbeitsmappe hinterlegt.