Mit folgendem Beitrag möchten wir die Unternehmensplanung anhand generativer Modelle (Bayessche Statistik) näher bringen und dabei Begriffe wie «Ambition» und «Prognose» auf eine erfrischend neue Art präsentieren. Sie werden erstaunt sein, dass ohne grosse Investitionen in Planungssuiten auch mit Excel und MC FLO eine moderne Planung, welche subjektive Einschätzungen mit Daten kombiniert, aufgestellt werden kann. Richtig durchgeführt ersetzt eine solche Planung in weiten Teilen auch das heute in vielen Unternehmen noch separat aufgestellte Risikomanagement (umgekehrt kann auch argumentiert werden, dass Risikomanager die Unternehmensplanung durchführen sollten).
Für Unternehmen bedeutet die Planung vereinfacht das Durchdringen der Prozesse, welche für die Erstellung der am Markt offerierten Dienstleistungen/Produkte benötigt werden - vom Umsatzstrom bis zu den Kosten - mit den Ziel, die für den Fortbestand relevanten Treiber zu identifizieren und so auszugestalten, dass der Unternehmenswert maximiert wird.
Hierbei ist anzumerken, dass die Zukunft unsicher ist und die in der Planung zu berücksichtigenden Zahlen Schwankungen um einen anfänglichen Planwert (=Risiken) unterworfen sein werden. Ein Unternehmen, welches etwa Produktionskapazitäten zu steuern hat, kann sich daher nicht allein auf Mittel – oder Erwartungswerte abstützen, sondern muss die volle Bandbreite aller möglichen Ausprägungen vorab einschätzen, um anhand von Wahrscheinlichkeitsüberlegungen die richtigen Entscheidungen treffen zu können. Hinzu kommt, dass bei der unterjährigen Steuerung Abweichungen von den Zielwerten (=Ambition) zu identifizieren und neues Wissen aufgrund der Datenlage für eine Prognose heranzuziehen ist.
Zur Lösung aller dieser Probleme liefert die moderne, von Bayes geprägte Statistik in Kombination mit der Monte-Carlo Simulation das notwendige Handwerkszeug (=Framework), um eine Planung robust, nach wissenschaftlichen Prinzipien, aber auch erfinderisch gestalten zu können.
Um auch hier allen mathematischen Formeln auszuweichen gehen wir vom folgendem Sachverhalt aus: Ein neu gegründetes Unternehmen möchte Reparaturdienstleistungen für Uhren in der Region A erbringen. Als Teilaufgabe soll das Management die Umsatzplanung für das erste Jahr aufsetzen. Da bisher keine Daten für das Unternehmen vorliegen, sind für die Planung Schätzungen beizuziehen.
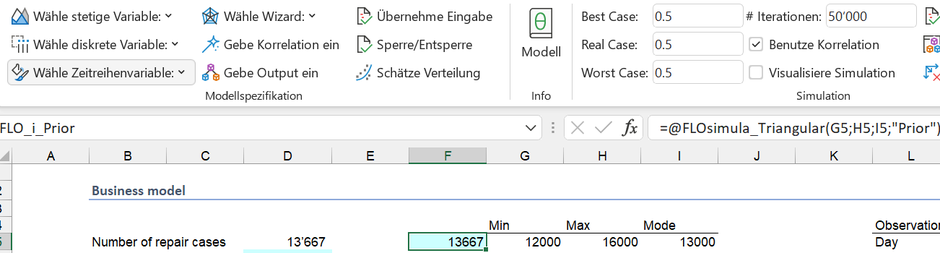
Gehen wir davon aus, dass das Management aufgrund der bisherigen Erfahrung aus der Uhrenbranche folgende Annahmen für ein Jahr (=240 Arbeitstage) aufgestellt hat, welche als Dreiecksverteilung vorliegt.
Das Management unterstellt, dass im Minimum 12'000 verrechnungsfähige Reparaturarbeiten innert eines Jahres durchgeführt werden, im Maximum 16'000 und am häufigsten 13'000. Diese «Schätzung» lässt sich als Wahrscheinlichkeitsverteilung darstellen und stellt im Sinne des Bayesschen Statistik unser Vorwissen («beliefs», «A-priori») dar.
Das erstmalige Aufsetzen einer Planung bedarf – bei Abwesenheit von Daten – das Beiziehen von Annahmen, welche quantifiziert werden.
Bezogen auf die Anzahl Reparaturaufträge, welche mittels einer Dreiecksverteilung hergeleitet wurde, ergibt sich folgendes Bild anhand einer Simulation:
Im Minimum werden 12'001 und im Maximum 15'970 Reparaturaufträge während eines Jahres berechnet, die Werte weichen also nicht erheblich vom theoretischen Minimum und Maximum ab. Weiterhin ist ersichtlich, dass 95% der Ergebnisse zwischen 12'320 und 15'463 liegen. Die Schwankungen zwischen dem Minimum und dem Maximum bildet die Unsicherheit ab. Dabei können tiefe Werte als Bestandteil von Worst-Case Szenarien, eine hohe Nachfrage als mögliche Ausprägung von Best-Case Szenarien aufgefasst werden.
Bei der Herleitung der Verrechnungspreise kann analog vorgegangen werden. So wird ein simpler Batteriewechsel anders bepreist als die Revision einer Uhr mit Tourbillon. Im Modell wurde der Preisstrom als Lognormalverteilung, also ebenfalls analytisch hergeleitet (Siehe Spalte B30ff). Nichts hält ein Unternehmen aber davon ab, bei den Annahmen eine benutzerdefinierte Funktion über ein Histogramm einzugeben. Hier liegt die grosse Flexibilität der Bayesschen Statistik begründet: Es gibt kein «wahr» oder «falsch», eher ein «gut begründet» und «weniger gut begründet». Wer es schafft bereits mit dem Aufsetzen der Planung die «richtigen» Schlüsse zu ziehen, wird bei der Steuerung vor weniger Probleme gestellt; aber auch «weniger gute» Annahmen lassen sich durch die im Zeitverlauf sich bietende Datenlage (dazu später mehr) anpassen*.
Eine robuste Planung deckt möglichst alle relevanten Sachverhalte ab. Oder anders: Ein Modell und somit die Aussagekraft einer Planung steht und fällt mit den Annahmen. Das Management muss sich somit mit den Beziehungen der Treiber untereinander als auch mit externen Faktoren auseinandersetzen. Gehen wir abschliessend davon aus, dass die Anzahl Reparaturen von der Erwartung zur Wirtschaftslage abhängt: geht es der Wirtschaft gut, werden die Konsumenten eher neue Uhren kaufen, als bestehende zu reparieren und umgekehrt. Diese Abhängigkeit kann numerisch als Korrelation aufgefasst werden und ist in Zelle D12 abgetragen.
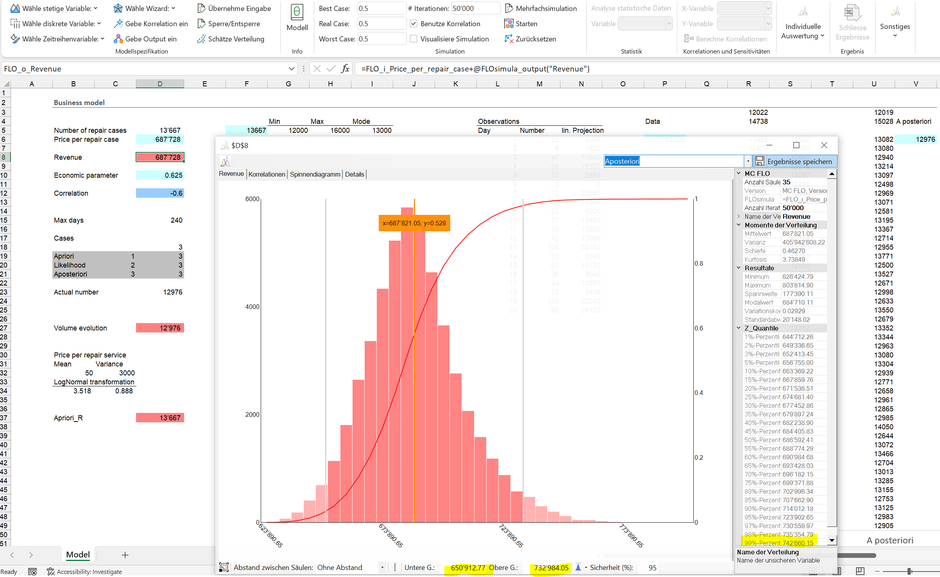
Als Steuerungsgrösse interessiert dem Management schlussendlich, welcher Umsatz im nächsten Jahr zu erwarten ist. Über das Produkt beider Grössen (Menge, Preis) kann der Umsatz gebildet und somit eine Vorhersage getroffen werden:
So sehen wir, dass 95% der Ergebnisse zwischen 0.65 MCHF und 0.82 MCHF liegen. Analog oben können wir somit folgende Aussage treffen: «Anhand der getroffenen Annahmen können wir zu 95% sicher sein, dass der Umsatz innert ein Jahr zwischen 0.65 MCHF und 0.82 CHF betragen wird». Die Resultate legen auch dar, was unter einer «Ambition» konkret zu subsummieren ist. Würde das Management ein Umsatzziel von 0.5 MCHF vorgeben, wäre die Wahrscheinlichkeit, dieses Umsatzziel zu übertreffen 100% und somit nicht ambitioniert (das simulierte Minimum von ca. 0.6 MCHF liegt über diesem Umsatzziel). Hingegen wäre ein Umsatzziel von 1 MCHF ambitioniert, aber nicht erreichbar.
Eine Ambition von 20% (oder anders: 80% der Ergebnisse liegen unter diesem Wert) bedeutet in unserem Fall, dass ein Umsatzziel von mindestens 766'000 CHF vorgeben wird. Dieses Ziel ist erreichbar, aber nur mit einer Wahrscheinlichkeit von 20%. Es ist Aufgabe des Managements im Vorfeld oder bei Vorliegen erster Zahlen konkret die Ambition und somit die Zielwerte festzulegen. Es kann und sollte diese Ziele sinnvollerweise nur aggregiert (etwa bei den Umsätzen), weniger bei den einzelnen Stellschrauben (Menge, Preise) vorgeben.
Geben wir davon aus, dass das Management eine Ambition von 30% festgelegt hat und somit ein Umsatzziel von ca. 748'000 CHF erwartet.
Die Planung, welches das Zusammenspiel der relevanten Treiber aufzeigt und Ziele vorgibt, ist somit in unserem Fall abgeschlossen (die Wirklichkeit ist naturgemäss komplexer [Verhalten Wettbewerber etc.]; aus Vereinfachungsgründen wird dies hier ausgeblendet). Sollen neue Treiber, etwa aufgrund eines erweiterten Geschäftsmodells, oder bisherige Treiber durch andere ersetzt werden, ist die Planung – also das Modell – anzupassen. Davon zu trennen ist die Frage, wann und wie die im Modell hinterlegten Grössen zwecks Messung der Zielerreichung zu aktualisieren sind.
Nach einem Monat (=20 Arbeitstage) liegen die ersten Daten zu den verrechnungsfähigen Reparaturaufträgen vor:
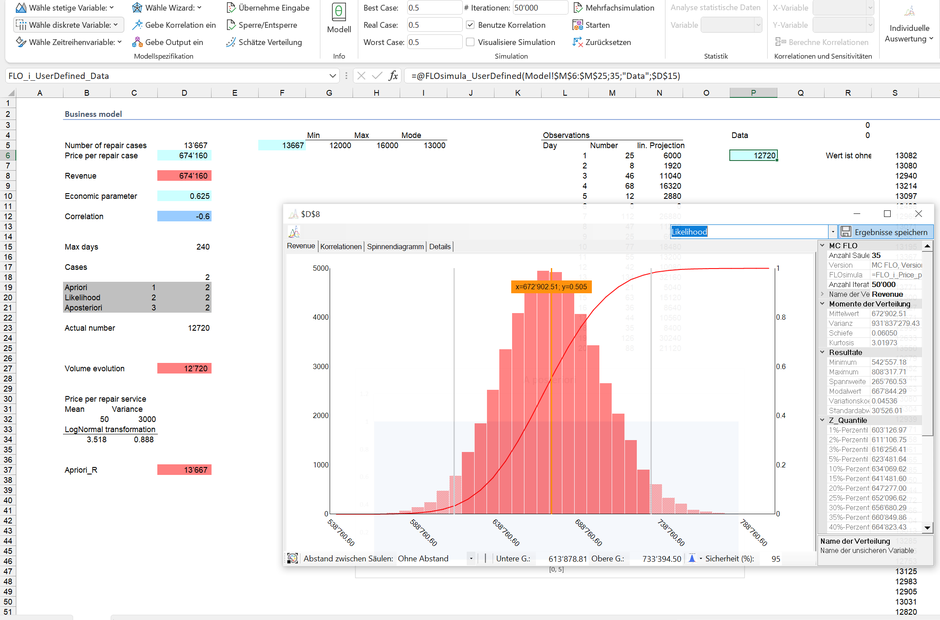
So wurden am Tag 6 keine Reparaturaufträge durchgeführt; die höchste gemessene Anzahl an Reparaturaufträgen an einem Tag beträgt hingegen 134 (Tag 13). Die Bayessche Statistik erlaubt uns die Daten («Evidenz») mit unserem Vorwissen zu kombinieren, um daraus ein angepasstes Wissen (A-posteriori) abzuleiten. Hierzu ist als erstes aus den Daten die Likelihood Funktion zu bestimmen. Das klinkt sehr technisch, ist aber für die meisten Planungsaufgaben relativ einfach umzusetzen. Die Idee ist folgende: Gegeben, wir hätten nur diese Daten und wir müssten eine Voraussage für ein Jahr machen, wie würden wir vorgehen? Der naive – und leider falsche Weg – besteht darin die einzelnen Ausprägungen linear auf das Jahr hochzurechnen und auf dieser Basis eine Verteilung zu generieren. Wenn wir 25 Reparaturaufträge pro Tag haben, dann folgt aus einer linearen Hochrechnung, dass nach einem Jahr insgesamt 6'000 (25 * 240) Reparaturaufträge durchgeführt worden sind. Die Wahrscheinlichkeit, dass an 240 Tagen hintereinander genau 25 Reparaturaufträge pro Tag auftreten, ist aber sehr gering. In den vorliegenden Daten aus 20 Tagen haben wir ja nur zweimal 25 Reparaturaufträge an einem Tag beobachten können. Gesucht sind somit Kombinationen, welche die voraussichtlichen beobachtbaren Werte maximieren. Das ist dann unsere Likelihood.
Anbei die entsprechende Likelihood Funktion nach einer Simulation mit 50'000 zufälligen -aber innerhalb der Spezifikation liegenden- Werten.
Aus der Likelihood Funktion wird ersichtlich, dass die voraussichtlichen Reparaturaufträge anhand der Daten zwischen 10'451 und 15'164 in einem Jahr schwanken dürften. In Kombination mit der Preisfunktion ergibt sich folgende Likelihood für den Umsatz (wir unterstellen vereinfachend, dass die Evidenz zu den Preisen und der Korrelation dem Vorwissen entsprechen):
In Bezug auf die Likelihood liegen 95% der Ergebnisse zwischen 0.61 MCHF und 0.73 MCHF; das Maximum bei gerade 0.81 MCHF.
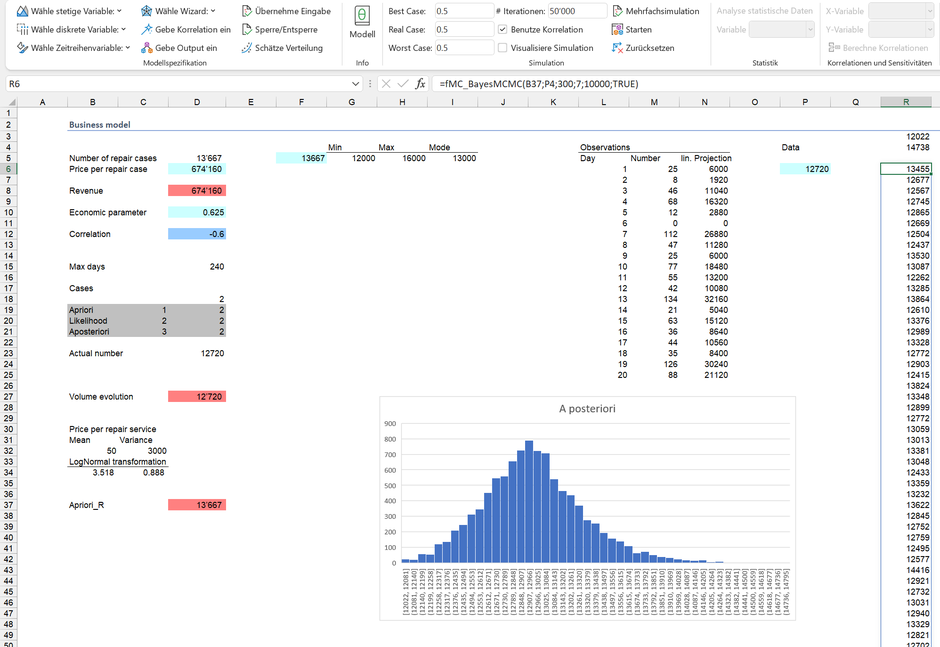
Als nächstes ist die Likelihood Funktion in Bezug auf dem Umsatz mit dem Vorwissen zu kombinieren. Diese Verteilung ist – wie das Vorwissen - für eine Prognose sodann nutzbar**.
Nach einer erneuten Simulation – in welcher das Vorwissen in Zelle D5 durch die A-posteriori Verteilung substituiert wurde, kommt folgendes Ergebnis zum Vorschein (wir unterstellen folgend, dass die Ergebnisse des Vormonats vollständig in der Aposteriori Verteilung enthalten sind):
In 95% der Fälle wird der Umsatz nach einem Jahr zwischen 0.65 und 0.73 MCHF liegen. Die Wahrscheinlichkeit, dass der Umsatz die Zielvorgabe von 0.77 MCHF überschreitet, beträgt neu hingegen weniger als 1% (die Bayessche Statistik kann sogar noch einen Schritt weitergehen und aus der A-posteriori Verteilung der Reparaturaufträge und der entsprechenden Likelihood eine Prognose der Reparaturaufträge für den nächsten Monat erstellen).
Für das Management stellt sich anhand der beobachteten Daten und der resultierenden A-posteriori Verteilung, ob es die bisher definierte Ambition weiterhin aufrechterhalten möchte oder aufgrund der Datenlage anzupassen hat. Die Entscheidung kann und darf keine Maschine abnehmen. Das Management kann einen weiteren Monat abwarten und aus den dann verfügbaren Daten eine erneute Kombination mit dem «Vorwissen» (vormalige A-posteriori Verteilung) vornehmen und eine aktualisierte A-posteriori Verteilung ermitteln. Es kann aber – bei Festhalten an der ursprünglichen Ambition – die Massnahmen definieren, welche zu einer Erhöhung der erwarteten Umsätze beitragen. Da es die externen Faktoren – wie die Einschätzung zur Wirtschaftslage – faktisch nicht beeinflussen kann, verbleibt in unserem Modellsetting nur die Anpassung der Preise als Handlungsoption.
Fazit: Die von Bayes geprägte Statistik in Zusammenspiel mit der Monte-Carlo Simulation kann hervorragend für die Unternehmensplanung beigezogen werden. Sie fusst auf dem Konzept des Vorwissens (A-priori), welches die subjektiven Einschätzungen quantifiziert und anhand von Daten eine Aktualisierung des Vorwissens erlaubt. Durch die Quantifizierung aller möglicher zukünftiger Zustände (Szenarien) können Ambitionen (Zielwerte) konsistent hergeleitet und Prognosen erstellt werden.
*Die moderne Risikoforschung zeigt auf, dass bei der Aufstellung des Vorwissens Menschen Verzerrungen ausgesetzt sind (etwa indem Wahrscheinlichkeiten falsch eingeschätzt werden). Dies trifft zwar zu, relativiert sich aber, wenn die Daten uns einen Spiegel vor Augen halten und gestützt darauf unser Wissen angepasst wird.
**Viele Menschen denken, dass wir uns nur auf die Daten - also hier der Likelihood - abstützen sollten. Dies ist aber klar im Sinne der Bayesschen Auffassung zu verneinen. Was ist, wenn die vorliegenden Daten noch nicht die ganze Wahrheit widerspiegeln? Genau hier liegt der Rückgriff auf das Vorwissen begründet. Im Zeitablauf werden die Daten - falls das Vorwissen nicht als «absolut» eingestuft wurde - überhand nehmen.
Anekdote: Die vom Pfarrer Thomas Bayes unabhängig von Laplace entwickelte moderne Statistik wurde erst nach seinem Tod publik. Eine Vermutung ist, dass Bayes sich gegen eine Veröffentlichung gestellt habe, weil der Übergang von Vorwissen mittels Daten zum angepassten Wissen mit dem Glauben an Gott in Widerspruch steht. Damit die berühmte Bayessche Formel Sinn ergibt, darf das Vorwissen nicht absolut sein, andernfalls können auch die besten Daten zu keinem angepassten Wissen führen. Mit anderen Worten: Es sind Zweifel an der Existenz von Gott notwendig, damit das Vorwissen anhand der Daten in ein angepasstes A-posteriori Wissen überführt werden kann.
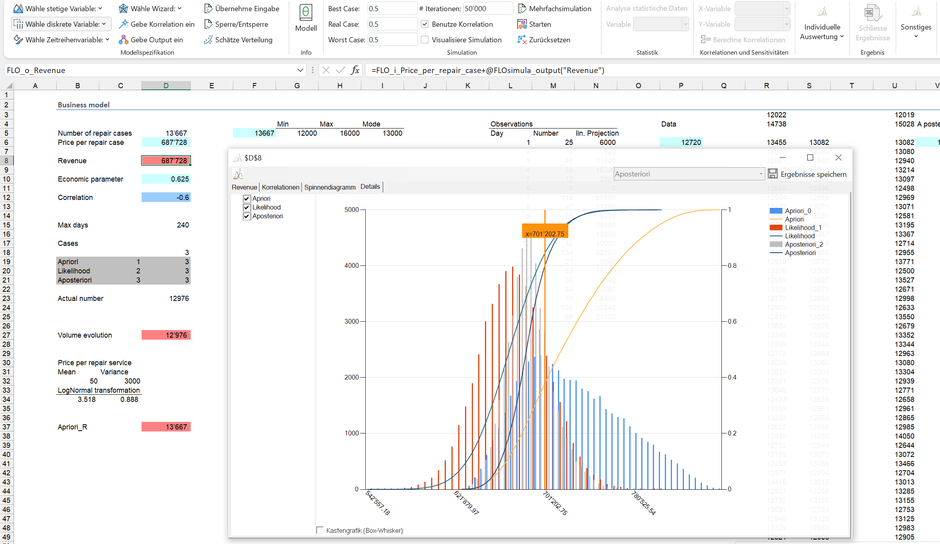
Anbei ein Vergleich der verschiedenen Verteilungen in Bezug auf den erwarteten Umsatz.
Anhand der Graphik kann die Ermittlung der A-posteriori Verteilung erklärt werden: Bei Werten, welche sowohl im Vorwissen als auch in der Likelihood vorkommen, ist die Wahrscheinlichkeit gross, dass diese in die A-posteriori Verteilung aufgenommen werden; hingegen sinkt die Wahrscheinlichkeit einer Aufnahme, falls die Werte differieren und weit auseinanderliegen. Die A-posteriori Verteilung stellt ein Kompromiss zwischen Vorwissen und gemessenen Daten dar.
Die hier vorgestellte Funktionen und das Beispiel-Excel stehen ab Version 7.6 von MC FLO zur Verfügung.
Update 01.09.2021: Einleitungstext angepasst.






Kommentar schreiben
Cornelius Nickert (Donnerstag, 02 September 2021 15:13)
toller Blog, bin gespannt auf das update. gibt es schon einen Termin dafür?