In der täglichen Praxis werden Monte Carlo Simulationen oftmals mit der Begründung fehlender Daten und mangelndem Wissen nicht eingesetzt. Wir denken, dass diese Ausrede zu kurz greift. Nein, sehr oft ist es wohl so, dass viele Leute - unbewusst - sich implizit an ein Gesetz klammern, dass die Monte-Carlo Simulation in weiten Teilen fasst überflüssig machen würde: dem Zentralen Grenzwertsatz.
Der Zentrale Grenzwertsatz besagt, dass eine Summe von sehr vielen unabhängigen identisch verteilten Zufallsvariablen mit endlicher Varianz approximativ normalverteilt ist.
Etwas einfacher formuliert klingt es so: In einem Modell gibt es sehr viele Variablen, die irgendwelchen Verteilungen folgen und von denen wir annehmen, dass diese – ganz wichtig - unabhängig voneinander sind. Wenn dies zutrifft, dann ist die gesuchte Grösse normalverteilt. Oder noch einfacher: Es sind die Mittelwerte der jeweiligen Verteilungen heranzuziehen, um den gesuchten Erwartungswert zu ermitteln.
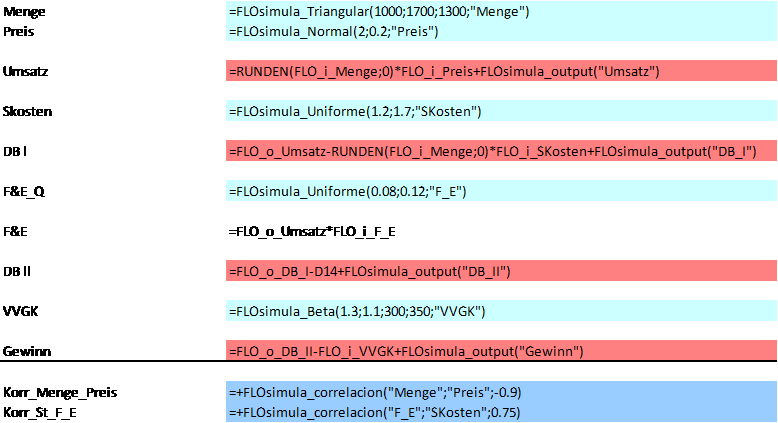
Sehen wir uns hierzu das folgende einfache Beispiel eines Geschäftsfalls der Unternehmensplanung an. Die gesuchte Grösse erwarteter Gewinn entspricht im Kern der Formel „(Menge * Preis) – (Stückkosten * Menge) – F&E – Verwaltungskosten“. Dabei wird beispielsweise die Zufallsvariable "Menge" anhand einer Dreiecksverteilung und die Variable "Stückkosten" anhand einer Gleichverteilung modelliert. Q
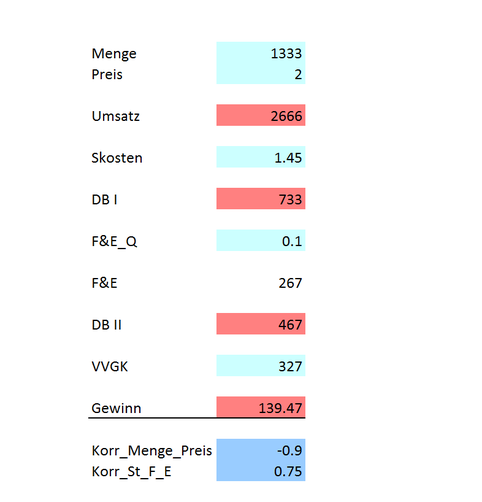
Ohne Simulation und unter Rückgriff der jeweiligen Mittelwerte der Verteilungen wird folgendes Ergebnis ausgewiesen:
Im Erwartungswert resultiert ein Gewinn von ca. 139 CHF. Bei der klassischen Planung würde der Modellierer auf die Berücksichtigung von Zufallsvariablen verzichten und nur den jeweiligen Erwartungswert ("Punktwert") heranziehen, etwa einen Preis von 2, um auf das gleiche Ergebnis zu kommen.
Eine Berechnung des Gewinns mittels Monte-Carlo Simulation mit 10‘000 Iterationen unter Einbezug der Zufallsvariablen zeigt folgendes Bild: das Ergebnis gleicht einer Normalverteilung - wie im Zentralen Grenzwertsatz beschrieben -, wobei der Erwartungswert des Gewinns ca. 137 CHF (also gerade mal ca. 2 CHF Abweichung) beträgt. Aufgrund der im Modell relativ geringen Anzahl von vier Inputvariablen ist die geringe Abweichung zu der gemäss Zentralen Grenzwertsatz postulierten Normalverteilung erklärbar.
In diesem Fall bringt die Monte-Carlo Simulation im Vergleich zur klassischen Berechnung anhand von Punktwerten so gut wie nichts. Dies unter der Voraussetzung, dass Sie nur am Erwartungswert (Mittelwert) der gesuchten Grösse interessiert sind.
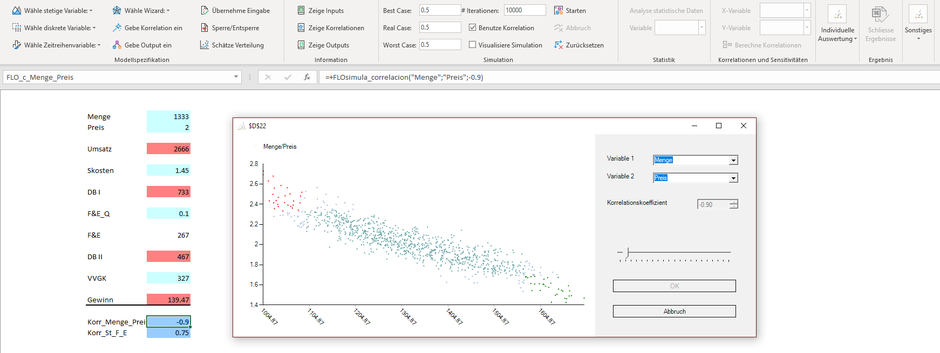
Die Realität verhält sich indes anders. So ist es fahrlässig anzunehmen, dass die Menge und der Verkaufspreis unabhängig voneinander sind. Auch ist nachvollziehbar, dass die Ausgaben für Forschung und Entwicklung besonders dann ansteigen, wenn gegenüber der Konkurrenz Wettbewerbsnachteile identifiziert werden, etwa aufgrund höherer Stückkosten. Gerade in diesem Fall schaffen Monte-Carlo Simulationen, welche einen funktionalen Zusammenhang zwischen den Zufallsvariablen berücksichtigen, Abhilfe. Die Idee besteht darin, eine Assoziation (Korrelation) zwischen zwei vormals unabhängigen Variablen zu definieren und diese bei der Simulation zu berücksichtigen.
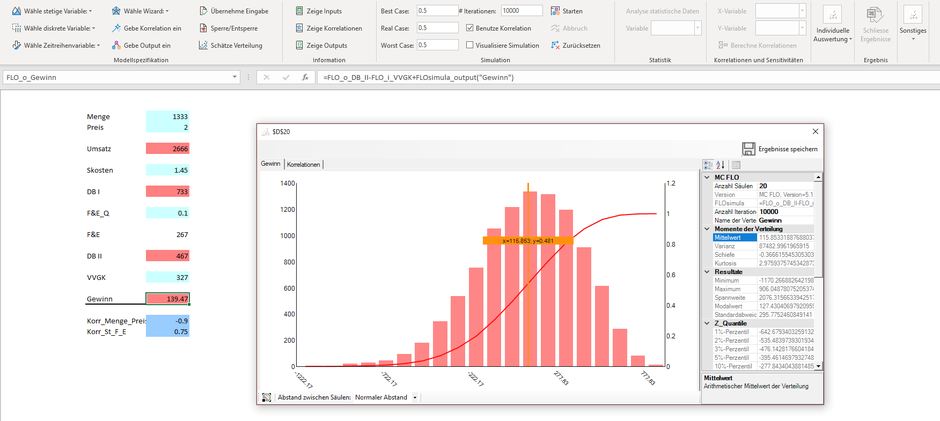
Mit der Berücksichtigung von Korrelationen im Modell (jeweils mit der Bezeichnung "Korr" im Tabellenblatt erfasst) verlassen wir somit die Grundannahmen des Zentralen Grenzwertsatz, welches unabhängige Verteilungen voraussetzt. Wird der Mittelwert immer noch bei 139 CHF liegen? Eine Simulation mit 10‘000 Iterationen und unter Berücksichtigung der Bildung von Korrelationen zwischen den Zufallsvariablen zeigt folgendes Bild: Der Gewinn liegt im Erwartungswert nun bei knapp 115 CHF, also knapp 17%! unter dem ursprünglichen Wert.
Im Vergleich zu oben hat die resultierende Verteilung – wie sichtbar - spürbar an „Schiefe“ gewonnen, was auf die Korrelation zwischen den definierten Inputvariablen Menge und Preis zurückzuführen ist.
Fazit: In einem Modell voller unabhängiger Variablen würde eine Monte-Carlo Simulation keinen grossen Erkenntnisgewinn bringen, wenn Sie nur am Erwartungswert der gesuchten Grösse interessiert sind. Die klassische Berechnung anhand von Punktwerten kommt zum gleichen gesuchten Ergebnis.
Die Umwelt ist jedoch voller Abhängigkeiten, die zu Fehlschlüssen beim Heranziehen von Punktwerten führen. Anhand des Fluchs der Mittelwerte haben wir zudem aufzeigen können, dass Punktwerte keine Aussage darüber zulassen, wie sicher das ermittelte Ergebnis eingestuft werden kann. Zudem ist es so, dass bei unternehmerischen Entscheidungen Mittel - oder Erwartungswerte kaum von Relevanz sind (Mittelwerte sind kaum für die Performance heranzuziehen, da wenig ambitioniert; für die Bemessung der Zahlungsfähigkeit ist zudem von einem worst case Szenario auszugehen).
Mit einer Monte-Carlo Simulation haben Sie hingegen ein Instrument, das einen Rundumblick erlaubt, so dass Sie bessere Entscheidungen treffen können.
Noch eine Nebenbemerkung: Assoziationen müssen im Modell nicht immer mittels expliziter Korrelationen berücksichtigt werden. Sehr oft entstehen Korrelationen unbewusst. Sobald wir etwa bei Zeitreihen eine Abhängigkeit zwischen den Jahren herstellen (etwa indem wir den Absatz des nächsten Jahres vom Absatz des laufendendes Jahres ableiten – Stichwort Autokorrelation), ist die vom Zentralen Grenzwertsatz postulierte Unabhängigkeit nicht gegeben. Leider bemerken das Excel und oft auch der Anwender nicht.


Kommentar schreiben