Eine gängige Suche über eine bekannte Suchmaschine mit den Stichwörtern "square-root-of time-rule" (englische Übersetzung dieser Pandora Box) bringt zu Tage, was wir geahnt hatten: Die Wurzel-T Regel kann nur in Ausnahmefällen, quasi unter Laborbedingungen angewandt werden.
Einleitend ist zu konstantieren, dass die Wurzel-T Regel eine Methode zur zeitlichen Skalierung eines Diffusionsprozess darstellt.
Was bedeutet es konkret? Hier der Versuch einer einfachen Darstellung. Stellen Sie sich vor, dass Sie an einem Montag den Materialbestand ihres Lagers für das Ende der Woche bestimmen möchten. Heute haben Sie 100 Teile auf Lager. Jeden Tag kann ein Teil hinzukommen oder eins vom Lager entnommen werden. Nach einem Tag haben Sie somit 101 oder 99 Teile. Wie sieht es nach 5 Tagen aus? Können es 95, 101 oder doch gar 105 Teile sein? Wenn wir die Teileveränderung eines Tages als Volatilität des Lagerbestandes interpretieren und diese mit 1% ansetzen, läge die Volatilität nach 5 Tagen unter der Annahme von Linearität somit bei 5% (also 1% mal 5). Wenn wir jedoch davon ausgehen, dass die Teilzufuhr oder Teileentnahme als unabhängiges Ereignis aufgefasst werden kann (oder anders ausgedrückt: jeden Tag wird neu gewürfelt), ist kaum davon auszugehen, dass in 5 aufeinanderfolgenden Tagen ausschliesslich der "schlechte" Zustand zum Vorschein kommt und wir somit am Ende der Woche nur noch 95 Teile haben. Die Multiplikation der Tagesvolatilität mit der Anzahl Tage ist augenscheinlich ein schlechter Schätzer. Es kann gezeigt werden, dass die Multiplikation der Tagesvolatilität mit der Wurzel der Anzahl Tage in diesem Fall der beste Schätzer der 5 Tages Volatilität darstellt.
Die Wurzel-T Regel als Skalierungsfaktor berücksichtigt, dass nur mit einer geringen Wahrscheinlichkeit nur gute oder nur schlechte Zustände in 5 aufeinanderfolgenden Tagen auftreten können - wie gesagt, Unabhängigkeit vorausgesetzt. In der Praxis bleibt die Wurzel-T Regel daher auf die Zeitreihe der geometrisch brownschen Bewegung reduziert. Ein Beispiel haben wir folgend in MC FLO dargestellt, bei der 100 Tage ausgehend von einem Preis von 100 simuliert wurden.
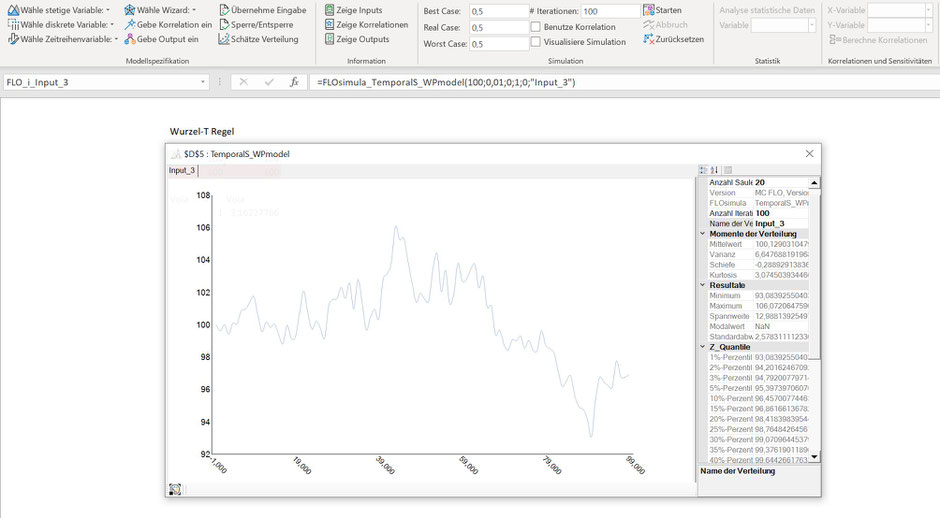
Wenn es nun alternativ möglich ist, dass die Teilentnahme mit der Zeit korreliert oder die Volatilität über den Zeitablauf unterschiedlich hoch ausfällt, kommt die Wurzel-T Regel schnell an ihre Grenzen und wird - gelinde gesagt - unbrauchbar. Daher ist beispielsweise bei der Prognose von Aktienkursentwicklungen besser auf andere Verfahren abzustützen.
Im folgenden Beispiel haben wir zwei Zeitreihen gegenübergestellt; die geometrisch-brownsche Bewegung (GBM) und den ARCH(1) Prozess, einmal für eine Haltedauer von 1 Tag und alternativ für 10 Tage. Nach einer Simulation mit 50'000 Iterationen sehen wir die resultierenden Volatilitäten (Standardabweichung) der beiden Verteilungen. Wie ersichtlich, beträgt die Volatilität der geometrisch-brownschen Bewegung) nach 10 Tagen genau der Volatilität eines Tages multipliziert mit dem Ergebnis aus Wurzel 10. Hingegen wird beim ARCH(1) Prozess eine Standardabweichung von ca. 1.81 berechnet, währenddem anhand der Wurzel-T Regel eine solche von 1 zu erwarten wäre.
DIe Wurzel-T Regel ist in der Praxis weit verbreitet, wie aber dargestellt an bestimmte Bedingungen geknüpft. Prüfen Sie daher die Voraussetzungen (Unabhängigkeit, konstante Volatilität), bevor Sie die Wurzel-T Regel anwenden.
In der Praxis werden zukünftige Ereignisse - etwa zur Bestimmung des Value-at-Risk - leider allzuoft anhand der Wurzel-T Regel bestimmt. Mit Simulationen können Sie aber darauf verzichten. Machen Sie es.
Update: Für den interessierten Leser ist beispielsweise folgender Artikel zur Wurzel-T Regel zu empfehlen: Diebold, Francis X. et al. (1998): "Converting 1-Day Volatility to h-Day Volatility: Scaling by Root-h is Worse than You Think," Wharton Financial Institutions Center, Working Paper 97-34.
Update: 22.11.2018: Einfaches Beispiel eingefügt.


Kommentar schreiben