«Beliefs» (Glauben) – Die Bayessche Statistik und Monte-Carlo Simulationen

Lange haben wir überlegt, wie wir die «moderne» Statistik, welche von Bayes geprägt wurde, ohne Formeln veranschaulichen können, auch im Wissen, dass vieles im Internet breit dokumentiert ist. Aber vielleicht – so unsere Hoffnung – kann etwas Erhellendes oder wenn auch nur die Spur von Bits und Bytes als Fussabdruck verbleiben.

Beginnen wir mit der klassischen – der frequentistischen – Auffassung der Statistik, wonach Wahrscheinlichkeiten allein durch Abzählen von Ereignissen im Ereignisraum entstehen. Nehmen wir das Beispiel des sechsseitigen, «fairen» Würfels. Die Wahrscheinlichkeit eine 5 zu würfeln beträgt 1/6, oder ca. 16.66%. Wir können dies durch eine Simulation nachvollziehen. In Excel haben wir 10'000 Würfe simuliert, nach dem 10'000 Wurf beträgt die gemessene Wahrscheinlichkeit 0.1652 (16.52%). Oder auch anders: in 10'000 Würfen wurde die 5 genau 1'625 gewürfelt. Eine weitere Simulation mit 10'000 Würfen würde ein nicht bedeutend abweichendes Ergebnis erzeugen. Würden wir die Simulation wieder und immer wieder vollziehen, ist im Mittel mit einem Wert von 1/6 zu rechnen.

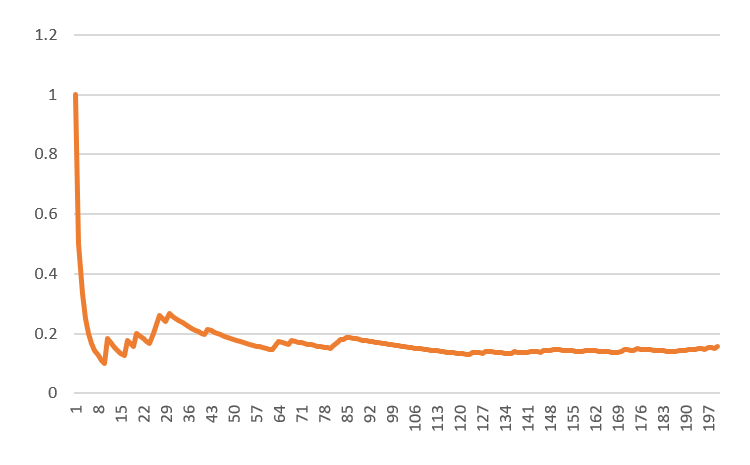
Die nachfolgende Graphik mit 200 Würfen zeigt auf, dass mit zunehmender Zahl von Würfen das Trefferverhältnis gegen die wahre Wahrscheinlichkeit von 1/6 «konvergiert». 

Wir können festhalten, dass die klassische Statistik zuallererst Messungen benötigt, um eine Aussage treffen zu können. Dabei gilt es zu betonen, dass Farbe und Konsistenz des Würfels (ob aus Holz geschnitzt oder aus Metall gefräst), der Ort und die räumliche Umgebung keine Rolle spielen. Ob auf der Eiger Nordwand oder unter sengender Hitze in der Wüste: die Wahrscheinlichkeit beträgt immer 1/6.

Wenn es aber darum geht, die Wahrscheinlichkeit des Wahlsieges von Donald Trump bei der nächsten Präsidentenwahl zu ermitteln, scheitert die frequentistische Auffassung, da es die nächste Präsidentenwahl mit Donald Trump als Kandidat nur einmal gibt und folglich nicht durch Messen mehrerer wiederholter und gleichartiger Ereignisse bestimmt werden kann.

Um hier Abhilfe zu schaffen, greift der Bayessche Wahrscheinlichkeitsbegriff auf «Vorinformationen» zurück und interpretiert die Wahrscheinlichkeit als Grad glaubwürdiger Erwartung. Als «Vorinformation» kann bestimmtes Vorwissen oder einfach auch nur eine Einschätzung einfliessen. Sobald neue Daten vorhanden sind, kann dieses Vorwissen aktualisiert und der Grad der persönlichen Überzeugung angepasst werden.

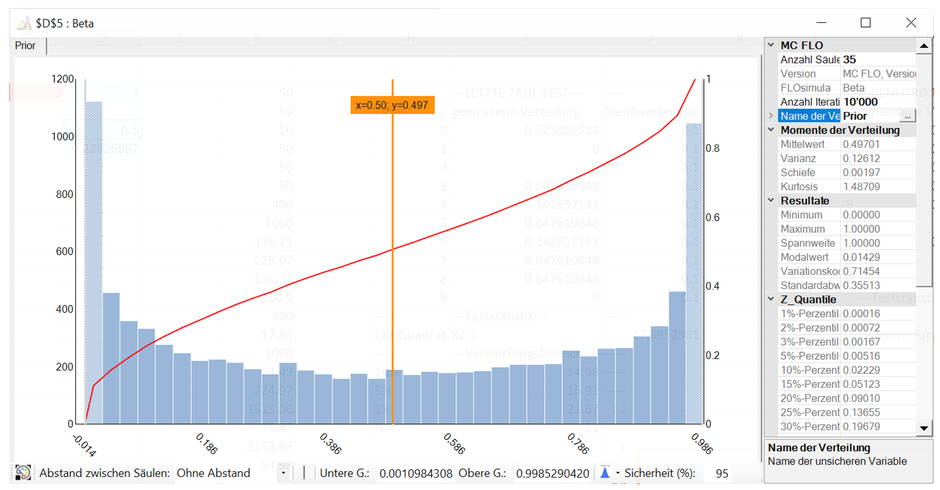
Stellen wir uns vor, dass wir ohne Kenntnis der genauen Form des Würfels (in Bezug auf die Seiten) die Wahrscheinlichkeit des Auftretens einer 5 schätzen müssen. Während der frequentistische Wahrscheinlichkeitsbegriff ein Vielzahl von Ereignissen voraussetzt, greift die Bayessche Auffassung - wie dargestellt - auf eine Vorkenntnis oder Einschätzung zurück, welche als Wahrscheinlichkeitsverteilung vorliegt. So könnten wir davon ausgehen, dass das Nichtauftreten als auch das alleinige Auftreten der 5 mit höherer Wahrscheinlichkeit einfliesst, alle anderen Ausprägungen hingegen als wenig plausibel eingestuft werden (diese Art der Verteilung ist als Jeffrey’s Prior bekannt).     

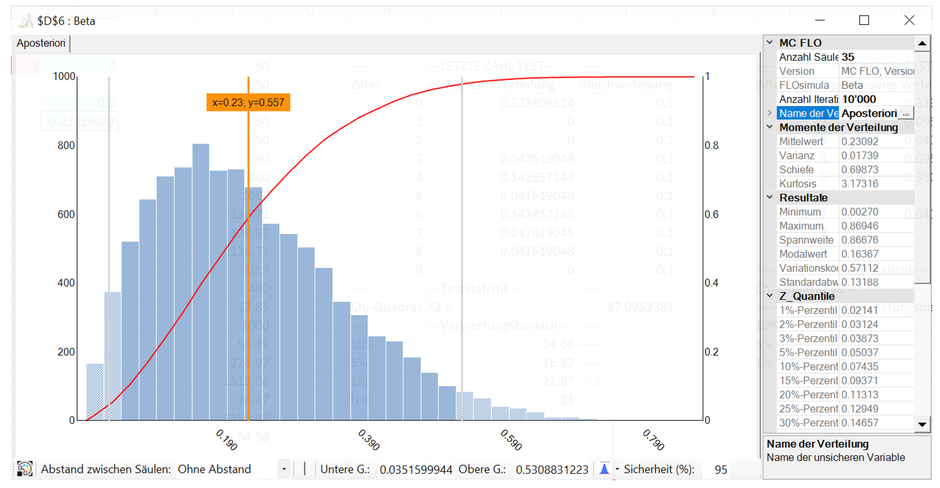
Mit jedem beobachteten Wurf passen wir die Verteilung an und erhalten somit eine neue Wahrscheinlichkeitsverteilung. Wir lernen also mit jedem Wurf. Endresultat ist die «a posteriori» Verteilung: im unteren Bild liegt der Modalwert der «a posteriori» Verteilung bei knapp 16%, der Erwartungswert bei 23%. Die Aussage kann dann wie folgt lauten: Aufgrund des Vorwissens und der gemessenen Daten besteht ein hoher Grad an persönlicher Überzeugung, dass die Wahrscheinlichkeit eine 5 zu würfeln bei 16% am Höchsten ist (der Weg vom Vorwissen [der «a-priori» Verteilung] zur «a posteriori» über die «Likelihood Funktion» ist durchaus kein leichter, kann aber für unsere weiteren Überlegungen übersprungen werden).

Im Kern greift der Bayessche Wahrscheinlichkeitsbegriff somit auf «subjektive» Einschätzungen (Glauben, oder um den englischen Begriff zu bemühen «beliefs») zurück. Die Einschätzung der Wahrscheinlichkeit, dass die 5 gewürfelt wird, kann je Vorwissen anders ausfallen. Dies unterscheidet sich fundamental vom frequentistischen Wahrscheinlichkeitsbegriff, bei der jede Messung eindeutig zum gleichen Ergebnis führt.

Bei Monte-Carlo Simulationen werden sowohl der frequentistische als auch der Bayessche Wahrscheinlichkeitsbegriff kombiniert. Die Modellbildung einer unsicheren Variable setzt voraus, dass diese über eine Wahrscheinlichkeitsverteilung beschrieben wird, wobei die Beschreibung auf «Vorwissen» oder auch «Expertenwissen» aufsetzt. Mit der frequentistischen Methode werden dann die gesuchten Ereignisse (etwa «Gewinn über Schwellenwert») ins Verhältnis zu allen Ausprägungen gesetzt, um daraus die Wahrscheinlichkeit oder auch hier Grad der Sicherheit zu ermitteln. Auch das Heranziehen der berühmten Formel von Bayes stellt kein Problem dar, etwa um die Wahrscheinlichkeit eines Gewinnes grösser 0 unter der Voraussetzung, dass die Absatzmenge einen bestimmten Schwellenwert überschritten hat, zu bestimmen.

Der grosse Vorteil der Monte-Carlo Simulation liegt darin, dass das subjektive «Bauchgefühl» auf einer objektiv nachvollziehbaren Grundlage gestellt wird und der Lernprozess dokumentiert bleibt. Mit jeder neuen Erfahrung des Managements wird das (erweiterte) subjektive Bauchgefühl rationalisiert und einer Kontrolle unterzogen.

Aus diesem Grund stellt es für die Bayessche Statistik kein Hindernis dar, wenn keine vorhandenen Daten für die Modellbildung eines bestimmten Sachverhalten vorliegen. Bereits allein auf Basis von Vorwissen oder auch Meinungen können Entscheidungsgrundlagen aufbereitet werden. Fehlende Daten, welche oftmals von den Kritikern einer Monte-Carlo Simulation herangezogen werden, sind im Lichte der Bayessche Wahrscheinlichkeitsauffassung keine Ausrede, um auf die Monte-Carlo Simulation zu verzichten.