Bei der Darstellung der Stolperfallen, welche in Zusammenhang mit der Multiplikation unter Unsicherheit auftreten können, sind wir vor Kurzem selber ins Stolpern geraten. Was war der Ursache für dieses Malheur?
Auch hier wieder an einem Beispiel erklärt. Stellen wir uns vor, dass ein Unternehmen einen Mindestumsatz erzielen muss, um profitabel zu sein (die Stückkosten sind fix). Es besteht Unsicherheit über die Absatzmenge und den Preis, der am Markt erzielt werden kann. Gleichzeitig sei unterstellt, dass zwischen Preis und Menge eine negative Korrelation beobachtbar sein sollte, was auf Wettbewerb oder andere Restriktionen am Markt zurück geführt werden kann.
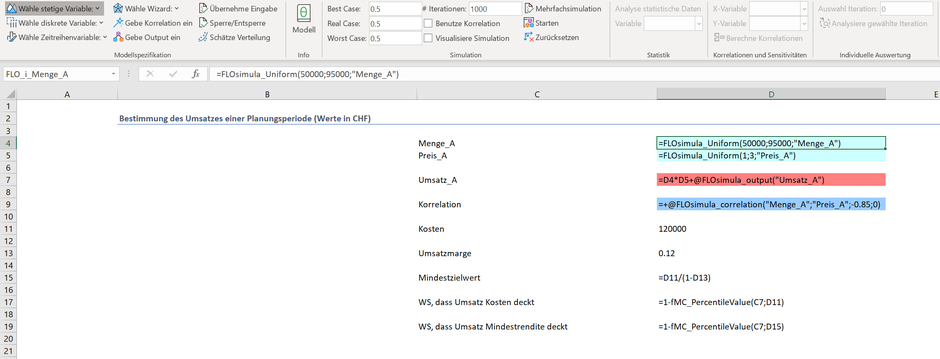
Das Unternehmen plant seinen Umsatz für die nächste Periode anhand des folgenden einfachen Modells:
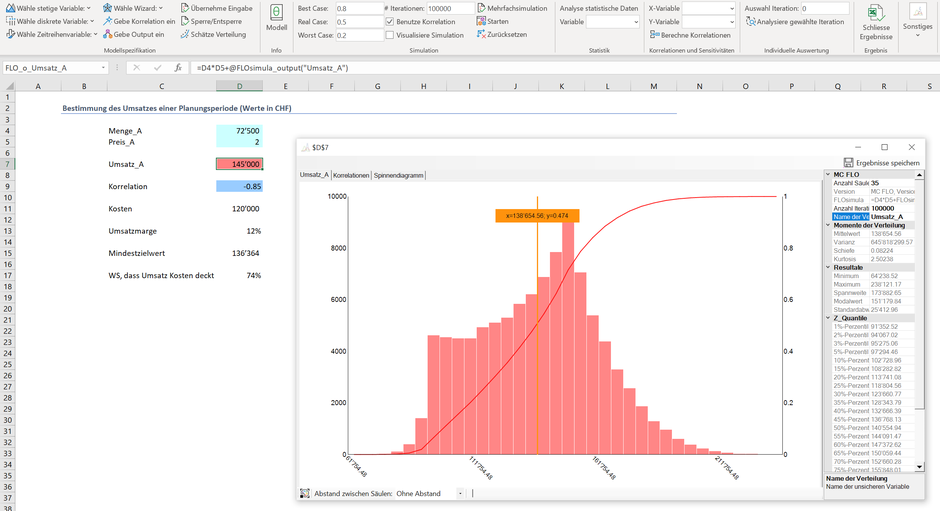
Gehen wir davon aus, dass die Kosten CHF 120'000 betragen, die Preise und Mengen - wie bereits formuliert - unsicher und jeweils mittels einer Gleichverteilung modelliert sind. Ein erste Simulation mit 100'000 Iterationen bringt folgendes Ergebnis hinsichtlich des Umsatzes zum Vorschein.
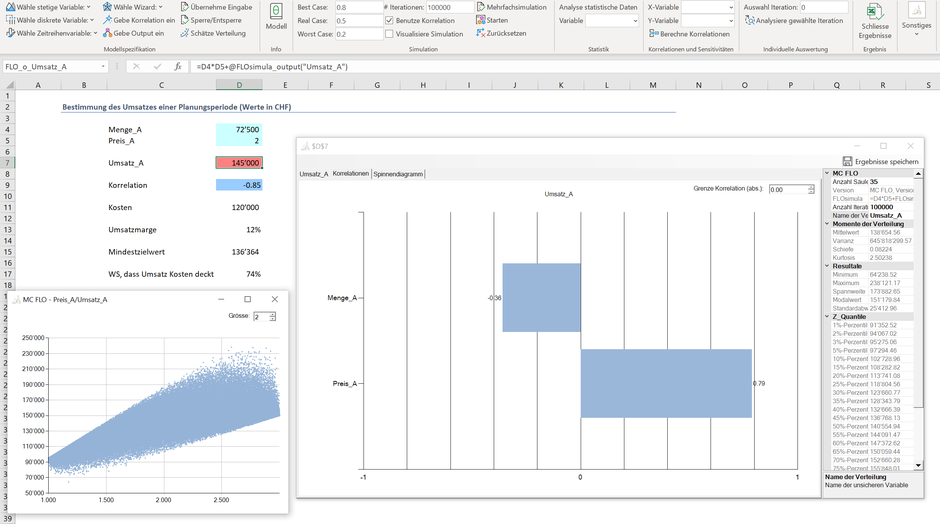
So sehen wir, dass der Umsatz in 74% der Fälle die Kosten von CHF 120'000 zu decken vermag, die Verteilung des Umsatzes hingegen sehr unförmig ist und aufgrund der unterstellten Korrelation begründet werden kann. Eine detailliertere Analyse zeigt auf, dass der Preis positiv mit dem Umsatz korreliert; dies obwohl der Preis mit der Menge vorab als negative Korrelation definiert wurde. Es erhellt, dass die Variable Preis in diesem Fall dominierend wirkt und für die Umsatzsteigerung eine Erhöhung des Preises in Erwägung gezogen werden sollte.
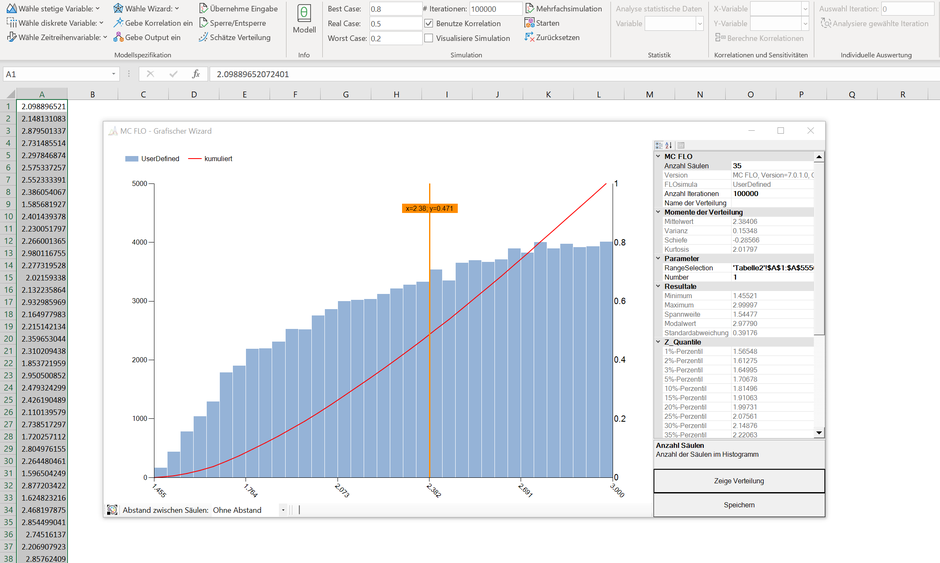
Trotz der Mächtigkeit von Simulationen dürfen wir eines nicht vergessen: Zu einem bestimmten Zeitpunkt muss das Unternehmen eine Entscheidung treffen. Es kann die Nachfrage nicht steuern, wohl aber den Preis. Die Bestimmung des Preises ist ein Akt unternehmerischer Freiheit und im Rahmen einer Planung als wesentlicher Bestandteil zu berücksichtigen, respektive zu verankern. Aber auch hier können und sollten uns Simulationen einen Weg vorzeichnen. Stellen wir uns verschärfend vor, dass das Unternehmen eine Umsatzrentabilität von 12% erzielen muss, um die anfänglichen Investitionen mit einer Mindestrendite zurück verdienen zu können. Der Zielumsatz beträgt somit mindestens CHF 136'364. Welchen Preis sollte das Unternehmen ansetzen? Ohne in die Abgründe der stochastischen Optimierung abzutauchen, reichen die bisher durchgeführten Berechnungen bereits aus. So sehen wir anhand der Streudiagramms auf der linken Seite, dass der Preis mindestens ca. CHF 1.45 pro Stück betragen muss, um den geforderten Mindestumsatz erzielen zu können. Um diesen zu validieren, exportieren wir in einem ersten Schritt alle Simulationsresultate und filtern diese nach den Zielumsatz. Anschliessend extrahieren wir aus dem gefilterten Datensatz alle Preise heraus, die zu diesem Zielumsatz beigetragen haben und laden diese Daten als benutzerdefinierte Variable ein.
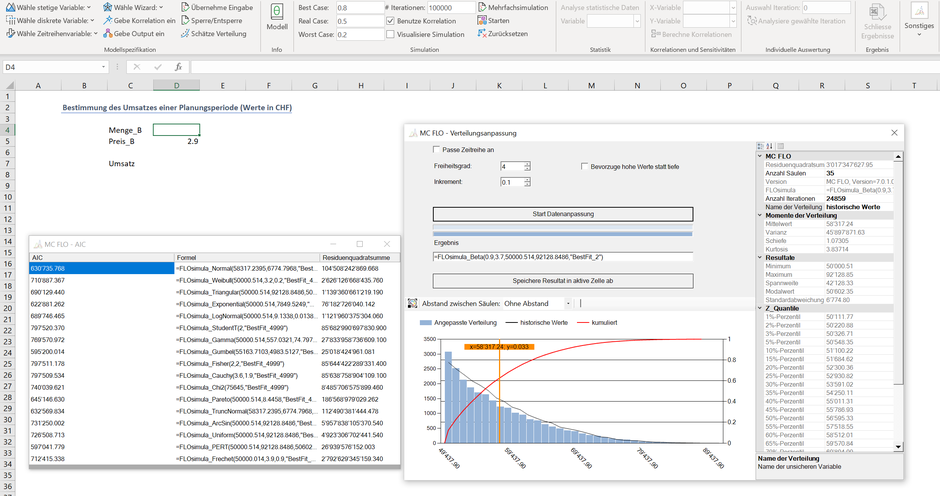
Wie ersichtlich ist der Modalwert am rechten Rand der Verteilung auszuloten. Das Management sollte daher die Preise hoch ansetzen. Gehen wir davon aus, dass das Management den Preis auf CHF 2.90 pro Stück fixiert hat. Wie sieht nun der erwartete Umsatz aus? Hierzu filtern wir aus dem Simulationsresultat alle Mengen heraus, welche bei einem Preis zwischen CHF 2.85 - CHF 2.95 nachgefragt werden. Anschliessend führen wir eine Verteilungsanpassung durch und setzen das Ergebnis als neue Verteilungsannahme für die Menge an.
Als Letztes vollziehen wir nochmals eine Monte-Carlo Simulation unter Einschluss des nun fixierten Preises. Der Umsatz ist dabei als Vielfaches der Inputgrösse Menge zu interpretieren.

Wir sehen nun, dass die Wahrscheinlichkeit eines Überschreitens des Mindestumsatzes von CHF 136'364 auf 100% angestiegen ist (das Minimum wird mit ca. CHF 145'000 ausgewiesen). Ist das Magie?
Halten wir fest: Im ersten Modell waren sowohl die Preise als auch die Mengen unsicher; die Korrelation zwischen diesen beiden Grössen aber als bekannt vorausgesetzt. Wir sahen, dass der Umsatz je nach Preis-Mengenkombination den erforderlichen Mindestumsatz zu überboten vermochte. Im Anschluss haben wir die Entscheidungssituation herbeigeführt und den Preis anhand der simulierten Ergebnisse und einer darauf aufsetzenden Optimierung festgelegt. Der festgelegte Preis ist umsatzmaximierend, da er die beste Reaktion auf die Preis-Mengenkombination darstellt. Als Residualgrösse verbleibt einzig die Unsicherheit über die nachgefragte Menge, welche über die Simulation hergeleitet wurde. Da selbst bei einem Preis von 3 CHF die nachgefragte Menge in unserem Modell mindestens 50'000 Einheiten beträgt, wird der Mindesumsatz mit Sicherheit erzielt. So viel zur Möglichkeit, mittels Simulationen auch eine Optimierung durchzuführen.
So weit, so gut. Als Kritik am urprünglichen Planmodell kann erwähnt werden, dass die Unsicherheit Unternehmen oftmals dazu drängt, ihre Preise ständig den Markterfordernissen anzupassen und daher die Fixierung eines Preises für die gesamte Planungsperiode als Relikt der "Old Economy" gilt. Besonders im Online Handel ist es sogar üblich, dass zur gleichen Zeit unterschiedliche Preise für das gleiche Produkt gefordert werden. Die im Ausgangsmodell vorgenommene Multiplikation von konstanten Preisen mit konstanten Mengen für jede einzelne Iteration der Simulation ist in diesen Fällen zu unterlassen und folglich das im vorliegenden Blogbeitrag beschriebene Verfahren der Konvulsion (oder auch Faltung) heranzuziehen. Hierbei ist die gesuchte Grösse (Umsatz) nicht als Produkt zweier Grössen, sondern als Summe zu bilden.
Um auf unser Ausgangsproblem zu kommen: Soll und darf die Multiplikation von zwei unsicheren Grössen (Preis, Menge) bei der Unternehmensplanung unter Anwendung einer Simulation Verwendung finden? Wenn Sie eine erste Auslegung machen, dann ist die Multiplikation je nach Geschäftsmodell zulässig. In allen anderen Fällen sollten Sie sich überlegen, ob nicht eine andere Darstellung sinnvoller ist. Schliesslich wollen wir, dass Sie bessere Entscheidungen treffen.

Kommentar schreiben