Haben Sie sich gefragt, warum Simulationsprogramme wie MC FLO die Student-t oder eine F-Verteilung anbieten, obwohl diese in der praktischen Handhabung mit Simulationen - etwa bei der Unternehmensplanung - kaum eine Rolle spielen? Wenn Sie neben Simulationen auch Hypothesentests durchführen, sollten Sie aufmerksam weiterlesen.
Gewiss, Simulationsprogramme sind nicht dazu erdacht klassische Statistikprogramme zu verdrängen. Für einfache Aufgaben reichen diese aber allemal. Anhand einiger Hypothesentests zeigen Ihnen folgend, wie Sie MC FLO sinnvoll dafür einsetzen können.
Vorab wollen wir kurz die Herangehensweise eines Tests rekapitulieren. Stellen Sie sich vor, dass Sie eine Stichprobe von 70 Erwachsenen gleichen Alters erhoben haben, welche am Tag mindestens 2 Stunden im Internet surfen. Bei den Probanden stellen Sie fest, dass deren IQ einen Wert von im Mittel 110 aufweist. Der Durchschnitt der gesamten erwachsenen Bevölkerung liegt bei 100. Ist der IQ von Erwachsenen mit Internetkonsum somit höher als der Durchschnitt von 100 oder ist der Wert von 110 aufgrund der Stichprobenvariabilität zurückzuführen?
Im Sinne des "in dubio pro reo" wird im Rahmen eines Testverfahrens als erstes die Nullhypothese aufgestellt. In unserem Fall lautet die Nullhypothese, dass der IQ-Mittelwert der Probanden 100 beträgt. Der ermittelte Wert von 110 sollte bei Gültigkeit der Nullhypothese nur auf die Stichprobenvariabilität zurückzuführen sein. Mit einem darauf folgenden Test sollen erhebliche Zweifel an der Gültigkeit der Nullhypothese aufgeworfen und somit die Nullhypothese verworfen werden. Da ein Test nicht mit absoluter Sicherheit die Nullhypothese verwerfen kann (im Sinne eines mathematischen Beweises), werden bestimmte Qualitätsanforderungen gestellt, welcher sich im alpha-Wert manifestiert. Falls das Resultat des Tests - genannt p-Wert - unter dem alpha-Wert von beispielsweise von 0.05 zu liegen kommt, lautet die Interpretation, dass wir mit einer Sicherheit (im Sinne einer Evidenz, Konfidenz) von 95% die Nullhypothese verwerfen können. Liegt der p-Wert hingegen über dem alpha-Wert, bestehen keine erheblichen Zweifel an der Gültigkeit der Nullhypothese. Sprich, läge im Fall der Studenten mit Internetzkonsumt der p-Wert bei 0.11 bei einem alpha-Wert von 0.05, wäre kaum davon auszugehen, dass Studenten mit Internetkonsum von 2 Stunden am Tag einen höheren IQ als der Durchschnitt aufweisen. Soviel zur Herangehensweise.
Die Kunst besteht darin, aus der Stichprobe und der gestellten Fragestellung den richtigen Test und die entsprechende Nullhypothese zu stellen. Folgende Fallbeispiele sind dem Buch: "Introduction to Statistics and Data Analysis", Fifth Edition Roxy Peck, Chris Olsen, Jay L. Devore, 2016 entnommen. Klicken Sie auf die Bilder, um den Sachverhalt und die Interpretation detailliert anzuschauen. Die Beispiele als Excel-Datei finden Sie hier. Darin sind die Problemstellungen detailliert ausgeführt. Im Folgenden wollen wir uns daher auf die wesentlichen Aussagen beschränken.
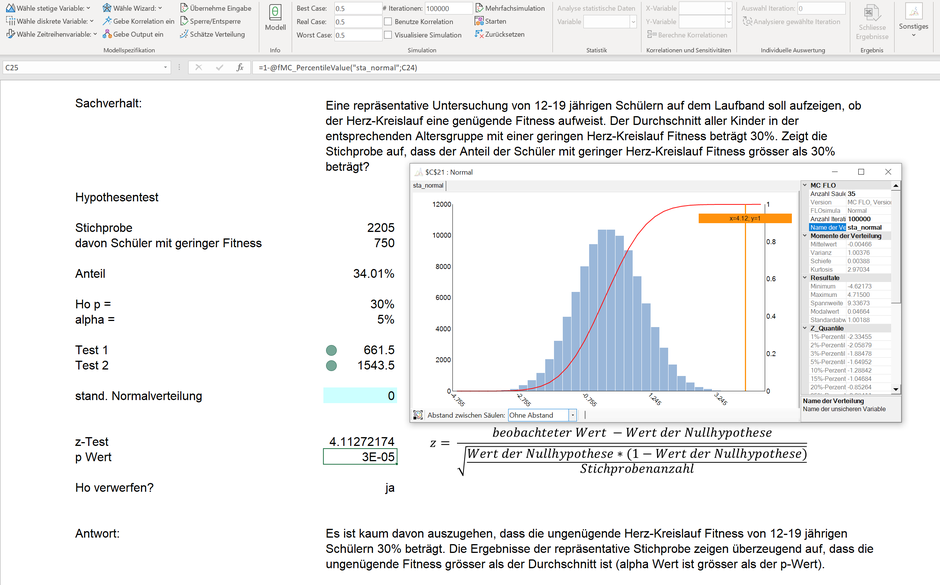
Fall 1: Hier wird die Fitness von Schülern untersucht. Es soll geprüft werden, ob der Fitnesswert der Stichprobe von 34.01% nur aufgrund der Stichprobenvariabilität vom durchschnittlichen Fitnesswert von 30% abweicht oder die Ergebnisse überzeigend darstellen können, dass die ungenügende Fitness über dem Durchschnitt liegt. Da wir die Grundgesamtheit kennen, wählen wir den z-Test und ziehen hierfür die Standardnormalverteilung heran. Der p-Wert ist nahe 0 und die Nullhypothese wird verworfen. Der entsprechende Sachverhalt und die Anwort im Detail sind dem folgenden Bild zu entnehmen.
Stellvertretend für alle Fälle hier die Erklärung für das Vorgehen: Bei der Ziehung einer Stichprobe - etwa über eine Befragung - sind wir am Mittelwert oder an Anteilen interessiert. Wird eine Stichprobe bei genügender Anzahl von Stichprobenelemente mehrmals wiederholt, nähert sich die Verteilung rund um den Mittelwert oder dem gesuchten Anteilen dem einer Normalverteilung. Sprich: bei den meisten Stichproben streut deren Mittelwert nur gering um den Mittelwert aller gezogenen Stichproben. Nur wenige Stichproben würden einen Mittelwert aufweisen, der erheblich vom Mittelwert aller Stichproben abweicht. Dabei ist zu berücksichtigen, dass die Verteilung der Mittelwerte "enger" als diejenige der Grundgesamtheit ist. Das wird mit dem z-Wert (oder auch z-Test) korrigiert. Der z-Wert gibt an, bei welchem Wert unser ermitteltes Ergebnis bei der Standardnormalverteilung zu liegen käme, der p-Wert die dazugehörige Wahrscheinlichkeit. Liegt der p-Wert unter dem angenommen alpha, ist die Nullhypothese zu verwerfen und die Alternativhypothese anzunehmen.
In unserem Fall liegt der z-Wert mit 4.11 am äusseren Rand der Standardnormalverteilung. Der ermittelte Anteil von 34.01% aus einer Stichprobe führt zu einem äquivalenten p-Wert von nahe Null. Die Nullhypthese ist daher zu verwerfen.
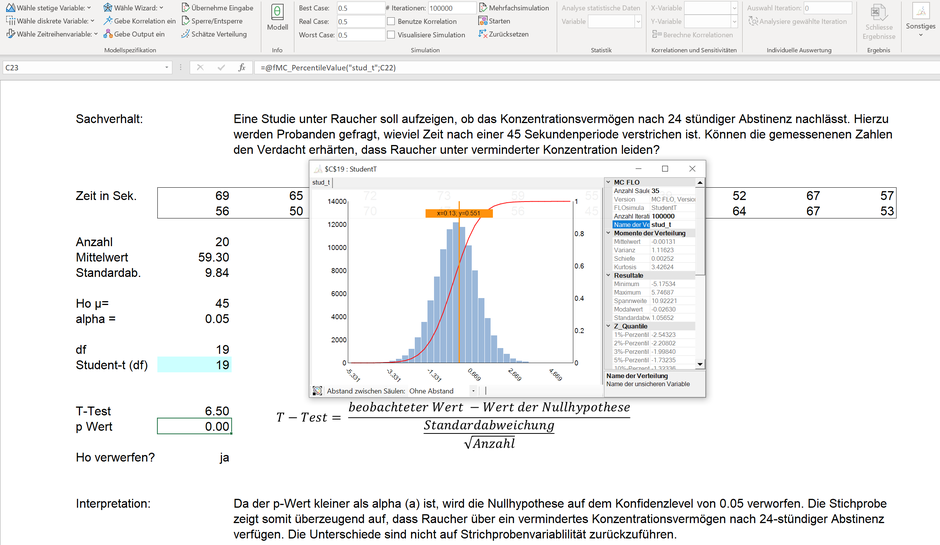
Fall 2 und 3: Hier wird der Durchschnitt einer Stichprobe untersucht. Da wir die Standardabweichung der Grundgesamtheit nicht kennen, wird der T-Test ausgewählt und ziehen hierfür die Student-t Verteilung mit (n-1) Freiheitsgraden heran.
Im Fall 2 liegt der höchste Wert einer Student-t Verteilung mit 19 Freiheitsgraden bei unter 5. Der untersuchte Wert von 6.5 ist nicht in der Student-t Verteilung enthalten. Der p-Wert ist somit 0.
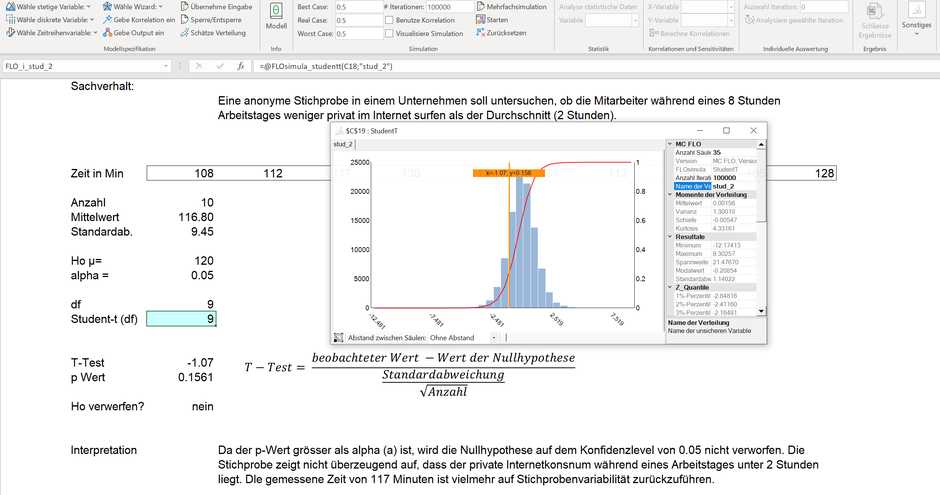
Im Fall 3 liegt der korrespondierende T-Wert der Student-t Verteilung mit 19 Freiheitsgraden bei -1.07 und somit relativ nah beim Mittelwert von 0. Der p-Wert beträgt 0.156 oder 16%. Der ermittelte Mittelwert von 116.8 Minuten Internetkonsum weicht daher nicht von der Nullhypthese (120 Minuten) ab.
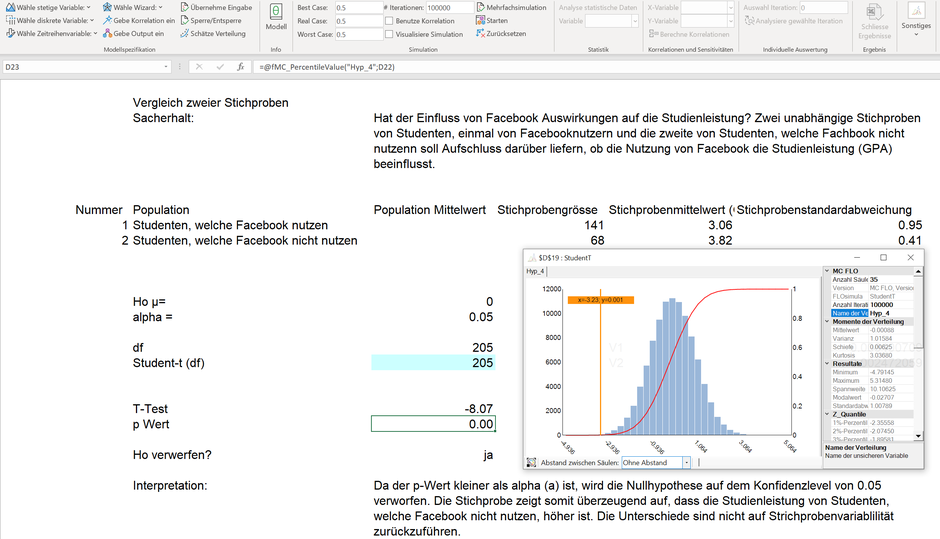
Fall 4: Es sollen zwei unabhängige Stichproben untersucht werden. Da wir die Standardabweichung der Grundgesamtheit nicht kennen, wird der T-Test ausgewählt und ziehen hierfür die Student-t Verteilung mit (n-1) Freiheitsgraden heran. Die Interpretation ist analog Fall 2.
So, das war der kleine Exkurs. Falls Sie eine Varianzanalyse von mehr als zwei Stichproben vornehmen wollen (ANOVA), können Sie auf den F-Test zurückgreifen. Das wollen wir Ihnen hier aber ersparen.
Hinweis: In allen Fällen setzten wir voraus, dass die Stichproben normalverteilt sind. Woher wissen wir aber, dass die Stichproben diese Eigenschaft aufweisen? Nehmen Sie den in MC FLO eingebauten Anderson-Darling Test, um schnell und unkompliziert einen Test vornehmen zu können.
P.S.: Die Berechnungen wurden mit der kommenden Version Fátima vorgenommen.

Kommentar schreiben