How to discover and prevent "sandbagging" using a simulation

Imagine that we have been given the responsibility to plan the costs of an arbitrary product, which is composed of several inputs from different departments. In particular, we have the task to plan the product costs so that we can assume with 90% certainty (or confidence) no overrun of the planned costs.

We assume that the product is composed of five services (raw materials, processing, finishing, marketing and sales / distribution) and that the costs vary between CHF 1 and CHF 10 for each service. We assume the costs as uncertain and uniform distributed.

We delegate the tasks to the individual departments. For the raw materials the following calculation is made: the minimum cost is CHF 1, the difference between of CHF 10 and CHF 1 weighted with the desired level of confidence must be added to the minimum in order to determine the required plan size for the raw materials. So (CHF 10 - CHF 1) * 0.9 + CHF 1 = CHF 9.10 results. This plan size is now passed on to the processing department. This will in turn make a similar calculation: for the reported 9.1 CHF, 1 CHF will be added as minimum costs and for the difference between 10 CHF and 1 CHF the required confidence level will be set again. This results in new plan costs of 18.2 CHF. Once we have reached sales / distribution, the final planned costs now amount to CHF 45.5.

Do you have any doubts? Most people would probably affirm the calculation. Well, whether we wanted to or not: with the described approach we have greatly overestimated the costs and thus described what "sandbagging" is about. Technically, "sandbagging" consists in accumulate large safety reserves which arise out of deliberate caution or, much more often, due to a lack of knowledge regarding the calculation rules under uncertainty.

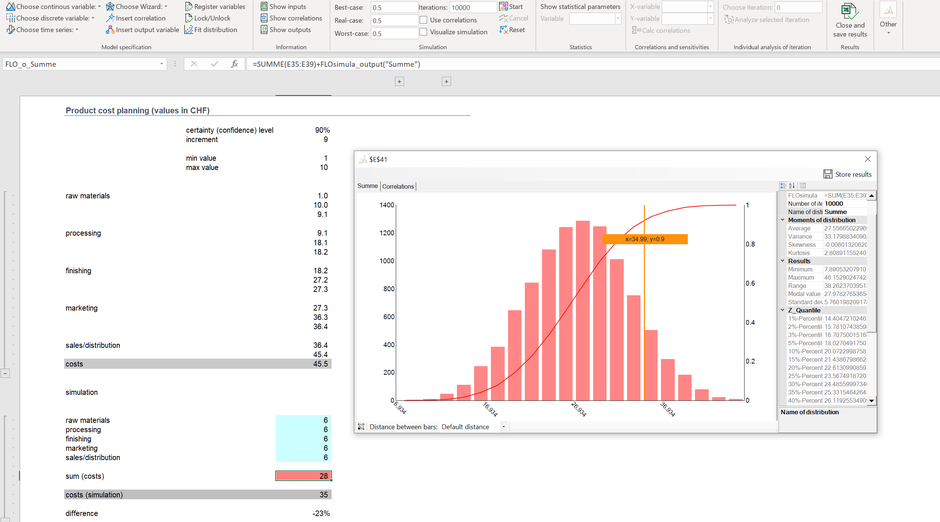
In the following we have described each uncertain event (costs between 1 and 10 CHF) as a random variable. At the bottom the sum is exposed. After a Monte-Carlo simulation with 10'000 iterations the planned costs at a security level of 90% are just CHF 35 and therefore 23% lower.

Why? The initial calculation assumes that the confidence level of 90% is reached each time. That is not realistic. It will be more likely (as an example) that the costs for the raw materials will be 10 CHF, whereas for costs for finishing remain at 3 CHF, etc. Due to the diversification effect of the central limit theorem the product costs are much lower at a certainty or confidence level of 90%.

We recommend to show transparently the uncertain events so that you can avoid "sandbagging". With a simulation you have the necessary instrument at hand.

P.S: This result can be obtained mathematically by using simple formulas and Excel. However, due to possible correlations and other factors we prefer to simulate rather than to calculate.