Decisions and simulations - beyond the risk of the Monty Hall problem

An analysis of annual reports published on the internet reveals that Monte-Carlo simulations are used to measure the remuneration of senior executives, to determine the value-at-risk of the portfolio, or generally to capture and to manage risks.

We are pleased that simulations are now widely accepted and even mentioned in the annual reports by name. As economists, however, we continue to be astonished that a simulation is often understood as an instrument that only comes into the scene after the decision has been made. In our opinion, a simulation is in contrast a decision-making tool, as it introduces a broad range of numbers into the discussion. An examination of the risks (threats and opportunities), derivated from the decision as a second step deprives the simulation of all potentials.

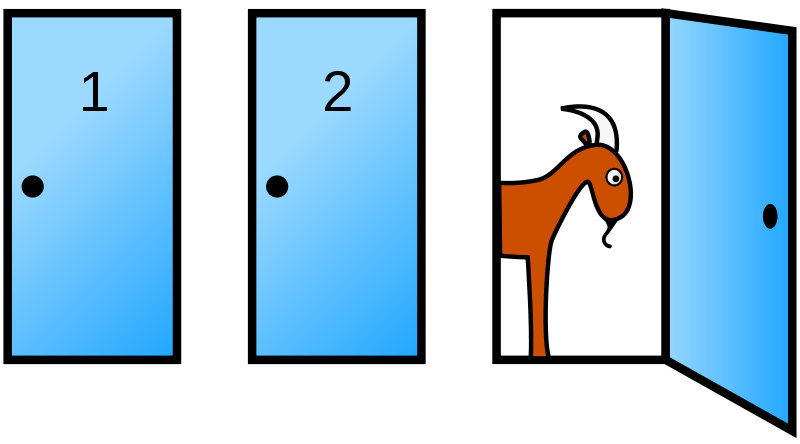
That brings us to the Monty Hall problem: in a game show a candidate stands in front of three locked doors. Behind one door is the main prize (a car), behind the other two doors stay goats. The candidate chooses one of the doors; The host opens one of the other two doors, behind which is with certainty a goat. The candidate may now reconsider his election. Should he stay with his original decision or choose another door?
Note: we refer here to the game where we compare the strategies between "always switching" or "alway staying".

Most people will probably consider the following: Once a door has been opened, two doors remain unopened. Behind one is the car, behind the other a goat. The chance that the car is behind the initially selected door is thus 50%. So switching should not bring any benefit.

However, the logically correct reasoning is different: At the beginning, one door has been selected from three, the chance of winning of that door is 1/3. The probability that the car is behind the two other doors (let's call the quantity of these two doors "B") is 2/3. Now the host opens one of these two doors from B, behind which there is with certainty a goat. So with a probability of 2/3 the remaining door of B wins.

The discussion concerning the thinking in probabilities and their strategic consequences is endless. Instead of using mathematical formulas, economists are more content with simpler procedures, such as those of a game, which is what the Monte-Carlo simulation is in essence. In addition, games make it easier to understand the rules and open the field for discussion.

The following shows the gameplay of the Monty Hall problem in Excel with MC FLO: First, the car is randomly assigned to a door based on a discrete uniform distribution. The candidate randomly selects one of these three doors, without knowing where the car is. The host then opens one of the doors, behind which is a goat. He chooses in our example always the door with the smallest number (canditate chooses door 2, car is also behind door 2, host opens door 1). Most of the Monte Carlo Excel add-ins should be capable to reproduce the Monty Hall problem.

If the car is behind the initially selected door and the candidate does not change, a 0 is reported as a hit; If the candidate changes and the car is behind the newly selected door, a 1 is reported as a hit. If we were to repeat the game hundreds or even thousands of times, how many times would the 0 or the 1 be accounted for a hit?

Enclosed the result after 1'000 iterations - et voilà, the Monte-Carlo simulation confirms that the chance of winning is 2/3. Switching is thus more advantageous.

To get back to the basic problem mentioned above, why should you set up a comprehensive risk management if you are sent home with the goat at the decisive moment?

Our advice: If you have been entrusted with the management of risks, make popular that simulations should be used in the decision-making process. After all, we want to make better decisions. That's what we call decision management.

See also "Grundlagen des Risikomanagements"; Werner Gleissner, Franz Wahlen, 3rd edition, 2016, which considers risk management as a system that "helps to create transparency about the scope of risk in the company and to support decisions under uncertainty by the management" [translated]. Since the term "risk" causes a negative reaction and is used inconsistently in the literature, we prefer to use the term decision.

The Monty Hall problem is also described on wikipedia: https://en.wikipedia.org/wiki/Monty_Hall_problem, as of february 2019.