In Anlehnung an unseren letzten Blog zur Unternehmensplanung wollen wir folgend in einer lange Sequenz das Prinzip der Bayesschen Statistik, der Likelihood und die praxisrelevante Anwendung im Kontext der Unternehmensplanung näher erläutern. Analog unserer bisherigen Abhandlungen wollen wir auf mathematische Formeln weitestgehend verzichten und anhand von Beispielen den Sachverhalt näher bringen. Unser Überzeugung nach kann nur so das mächtige Instrument der Bayesschen Statistik einer breiteren Bevölkerung näher gebracht werden. Wer vertiefte Informationen benötigt, kann auf das Onlinebuch «Bayes Rules!» (Bayes Rules! An Introduction to Bayesian Modeling with R (bayesrulesbook.com) von Alicia A. Johnson, Miles Ott, Mine Dogucu zurück greifen. Zum besseren Nachvollzug werden wir daher auch einige der dort aufgeführten Beispiele und die Beispiele aus diesem und dem nachfolgenden Blog hier («Bayes_rules.xlsx»)wiedergeben. Sie können die meisten der folgenden Beispiele somit direkt im Excel nachvollziehen.
Anbei (und damit hört es aber dann auch fast auf) die berühmte Formel von Bayes:
Einführendes Beispiel - Das Berufsorchester
A und B stehen hier für Aussagen, etwa A = «Person spielt in einem Berufsorchester» und B = «Person spielt mindestens 4 Stunden am Tag ein Instrument». Das Zeichen «|» ist als «gegeben, dass» zu interpretieren. P(*) steht für die Wahrscheinlichkeit. Dabei interpretieren wir die Wahrscheinlichkeit als Grad der glaubwürdigen Erwartung, welche insbesondere in Relation zu anderen Ereignisse aufzufassen ist. Aus der Aussage A «Person spielt in einem Berufsorchester» folgt, dass P(A) der (Ursprungs-)Wahrscheinlichkeit entspricht, wonach «Person in einem Berufsorchester» spielt. Diese Wahrscheinlichkeit liegt offenkundig zwischen 0 und 1 (0% und 100%). Für einen Betrachter ist die Aussage, dass die Wahrscheinlichkeit 90% beträgt, mit der Relation verbunden, wonach die Trefferquote eine Person auszuwählen, welche die gewünschte Eigenschaft aufweist, neunmal höher als ist der Fall, in der eine ausgewählte Person die gewünschte Eigenschaft nicht aufweist.
Gemäss der Bayesschen Formel und den definierten Aussagen für A und B entspricht P(A|B) der Wahrscheinlichkeit, dass eine Person in einem Berufsorchester spielt, gegeben dass diese Person mindestens 4 Stunden am Tag ein Instrument spielt».
Eine Internetsuche legt zu Tage, dass es in Deutschland über 130 Berufsorchester mit ca. 10'000 Mitglieder gibt. Bezogen auf die Anzahl von ca. 69.5 Mio. der erwachsene Bevölkerung Deutschlands (wir ignorieren, dass auch Minderjährige in einem Berufsorchester spielen) ergibt sich eine glaubwürdige Wahrscheinlichkeit P(A) von ca. 0.014% (10'000 / 69'500'000, jeweils Stand Ende 2020). Würden wir – ohne weitere Informationen – eine beliebige erwachsene und in Deutschland beheimate Person herauspicken, würden wir ihr eine Wahrscheinlichkeit von ca. 0.014% attestieren, dass diese Person in einem Berufsorchester spielt. Eine andere Herangehensweise an die Wahrscheinlichkeit ist, wonach die Behauptung, dass unter 10'000 zufällig ausgewählten erwachsene und in Deutschland ansässige Personen ca. 2 Personen in einem Berufsorchester spielen, nicht abwegig ist.*
Anders gestaltet sich der Sachverhalt, wenn wir in Bezug auf eine Person wüssten, dass diese mindestens 4 Stunden am Tag ein Musikinstrument spielt. Durch Kenntnis einer bestimmten und mit A in Zusammenhang stehenden Ereignis formt sich unser Wissen neu. Die Frage «Wie hoch ist die Wahrscheinlichkeit, dass eine Person in einem Berufsorchester spielt, gegeben dass diese Person mindestens 4 Stunden am Tag ein Musikinstrument spielt» kann dabei auf den einfachen zusammengesetzten Ausdruck P(A|B) reduziert werden. Der rechte Teil nach dem Gleichheitszeichen der obigen Bayes Formel zeigt dann auf, wie wir zu Lösung kommen. Doch bevor noch ein paar Gedankenübungen.
Stellen wir uns weiters vor, dass wir eine Aussage C «Person hat blaue Augen» haben. Der zusammengesetzte Ausdruck P(A|C) fragt somit nach der Wahrscheinlichkeit, dass eine Person in einem Berufsorchester spielt, gegeben dass diese Person blaue Augen hat. Intuitiv nehmen wir richtigerweise an, dass die Augenfarbe keinen Einfluss auf die Wahrscheinlichkeit, ob eine Person in einem Berufsorchester spielt oder nicht, hat. P(A|C) ist in diesem Fall somit P(A). Die Bayessche Statistik ergibt somit nur dann einen tiefen Sinn, wenn Aussagen zusammengesetzt werden, die in einem Zusammenhang stehen. Im Kontext der Unternehmensplanung ist beispielsweise der Zusammenhang zwischen Gewinn (Aussage A) und Absatzmenge (Aussage B) und/oder zwischen Gewinn (Aussage A) und Kosten (Aussage C) von Relevanz. Die Kernidee liegt darin Aussagen von "x" zu finden, die unser Verständnis von A schärfen. Dabei kann P(A|x) im Vergleich zu P(A) zu einer Erhöhung oder auch zu einer Senkung der Wahrscheinlichkeit führen. Nehmen wir hier ein im zitierten Online-Buch aufgeführtes Beispiel. Ohne Vorkenntnis oder allein auf Basisinformationen zurückgreifend, können wir die Wahrscheinlichkeit ermitteln, ob eine Person die Grippe hat (Ereignis A). Wenn wir aber nun zusätzlich wüssten, dass diese Person sich ständig die Hände wäscht und kaum aus dem Haus geht (Ereignis X), würden wir dieser Person eine geringere Wahrscheinlichkeit zutragen, an Grippe erkrankt zu sein. P(A) ist in diesem Fall grösser als P(A|X). Noch einmal: Wenn wir ein Ereignis X beobachten, welches mit A in Zusammenhang steht, dann gilt P(A|X) <> P(A), wobei «<>» mit «ungleich» gleichzusetzen ist.
Tasten wir uns nun an den rechten Teil der Gleichung heran. P(B|A) entspricht in unserem Beispiel der Wahrscheinlichkeit, dass eine Person mindestens 4 Stunden an einem Tag spielt, gegeben dass diese Person in einem Berufsorchester spielt. Es gilt im Regelfall, dass P(A|B) <> P(B|A) ist. Schauen wir uns dies genauer an. Es gibt gute und weniger gute Berufsorchester, aber auch weniger und sehr talentierte Musiker. Es kann daher durchaus sein, dass einige Berufsmusiker nur maximal 4 Stunden am Tag spielen und den Rest des beruflichen Alltags mit Studium der Noten, Verwaltungstätigkeiten oder gar mit dem Komponieren verbringen. Gehen wir davon aus, dass etwa 250 der ca. 10'000 Berufsmusiker maximal 4 Stunden am Tag ein Instrument spielen, 9'750 aller Berufsmusiker spielen somit mindestens 4 Stunden am Tag ein Instrument. P(B|A) entspricht daher 97.5% (9’750/10'000).
Um zur Antwort von P(A|B) zu kommen, müssen wir in der Gleichung oben noch P(B) ermitteln, also die Wahrscheinlichkeit, dass eine Person mindestens 4 Stunden am Tag ein Instrument spielt. Wer denkt, dass die Anzahl aller Personen, welche mindestens 4 Stunden am Tag ein Instrument spielt 9'750 (10'000 – 250) entsprechen müsse, irrt. Es kann ja gut sein, dass einige Personen aus der erwachsenen Bevölkerung nur aus Eifer oder zur Belustigung mehr als 4 Stunden am Tag ein Instrument spielen oder einer anderen beruflichen Aktivität ausserhalb eines Berufsorchester nachgehen, etwa als Musiker in einer Band oder in einem Zirkus. Nehmen wir an, dass wir auch diese Zahl kennen. Bei angenommen 25'000 erwachsenen und in Deutschland beheimatete Personen, welche mindestens 4 Stunden am Tag spielen, beträgt P(B) ca. 0.036% (25'000 / 69'500'000). Würden wir – ohne weitere Informationen – eine beliebige erwachsene und in Deutschland beheimate Person herauspicken, würden wir ihr eine Wahrscheinlichkeit von ca. 0.036% attestieren, dass diese Person mindestens 4 Stunden am Tag ein Instrument spielt. Unsere Antwort auf die Ursprungsfrage P(A|B) entspricht dann durch Auflösung der Gleichung oben 0.014% * 97.5% / 0.036% = 39%. Oder mit Worten: Die Wahrscheinlichkeit, dass eine Personen in einem Berufsorchester spielt, gegeben dass diese Person mindestens 4 Stunden am Tag mit einem Instrument übt, beträgt 39%.
Ohne weitere Kenntnis über die Person, betrug die anfängliche Wahrscheinlichkeit, dass diese Person in einem Berufsorchester spielt, gerade 0.0145%. Nachdem wir Kenntnis erlangt haben, dass diese Person mehr als vier Stunden in einem Berufsorchester spielt, ist diese Wahrscheinlichkeit auf 39% angestiegen!
Noch einfacher geht es mittels einem Entscheidungsbaum und den natürlichen Häufigkeiten, wie folgend abgebildet. In jedem Ast ist die Eigenschaft (etwa «Anzahl Personen in einem Berufsorchester») einzutragen, am Ende des Blattes (Knoten) wird die entsprechende Zahl hinzugefügt. Dabei entspricht der Summe der Knoten je Ebene dem Betrag des darüber liegenden Knotens. Die gesuchte Grösse kann durch die Bildung der natürlichen Häufigkeit ermitteln werden. Wir haben 9'750 Personen, welche mehr als 4 Stunden ein Musikinstrument spielen und in einem Berufsorchester sind. Die Anzahl Personen, welche insgesamt mehr als 4 Stunden ein Musikinstrument spielen, beträgt 25'000. Das Verhältnis beider Grössen entspricht unseren 39%!
Der grosse Vorteil der oben dargestellten Formel und der Bayesschen Statistik liegt in seiner grosser Flexibilität sowohl hinsichtlich der zu wählenden Ereignisse oder des innewohnenden subjektivem Empfinden von Wahrscheinlichkeiten. Der Reihe nach.
Fragen wie «Wie hoch ist die Wahrscheinlichkeit, dass es auf dem Mond Leben gibt, gegeben dass dort Wasser gefunden wird» ist eine zulässige Formulierung gemäss obiger Formel, wie auch die Frage "Wie hoch ist die Wahrscheinlichkeit, dass eine erwachsene Person sich in intensivmedizinische Betreuung begeben muss, gegeben dass diese gegen Covid-19 geimpft ist". Die Bayessche Statistik beschränkt sich somit nicht allein auf bereits bekannte Tatsachen (was in der klassischen frequentistischen Auffassung der Statistik durch den Beizug wiederholter Experimente gefordert ist), sondern erlaubt ein Zusammenführen von Ereignissen, welche noch nicht abschliessend beobachtet wurden oder gar vollständig in der Zukunft liegen.
Die Ereignisse können Hypothesen, Theorien und allgemein eine bestimmte Datensammlung umfassen. Daher können auch Metaereignisse wie «Wie hoch ist die Wahrscheinlichkeit, dass meine Hypothese zutrifft, gegeben dass eine Stichprobe vorliegt?» zusammengesetzt werden.
Sie werden sich aber sicher schon gefragt haben, woher die Zahlen von P(A) und P(B) als auch P(B|A) kommen sollen, wenn diesbezüglich keine Daten vorliegen. Tja, ganz einfach: Wenn keine Zahlen vorliegen, simulieren Sie diese. Und schon sind wir bei unserem Beispiel aus der Planung.
Erweitertes Beispiel - Die Umsatzplanung einer Eisdiele
Stellen Sie sich vor, dass Sie als verantwortliche Person einer Eisdiele die Planung für den nächsten Monat aufzustellen haben. Leider sind alle bisherigen Daten verloren gegangen, so dass Sie auf Einschätzungen oder allgemein auf Vorwissen zurückgreifen müssen. So nehmen Sie an, dass die Absatzmenge als PERT Verteilung mit einem Minimum von 2’200, einem Maximum von 5'000 und einem wahrscheinlichsten Wert von 4'500 Eiskugeln dargestellt werden kann. Ihr subjektives Empfinden wird durch die Überführung in eine Wahrscheinlichkeitsverteilung (hier PERT) in eine objektiv nachvollziehbare Kalkulation überführt. Die Kosten als auch der Absatzpreis (3.50 CHF pro Eiskugel) werden als fix angenommen. Aus Ihrer Erfahrung wissen Sie, dass bei gutem Wetter mehr Kugeln verkauft werden als bei schlechtem. Das Wetter wird Ihrem Anschein mehrheitlich gut, aber es kann auch gut sein, dass der nächste Monat teilweise regnerisch ausfallen wird. Um diese Unsicherheit einzufangen, modellieren Sie die Wetterprognose für den nächsten Monat anhand einer Beta Verteilung. Die Abhängigkeit zwischen Wetter und verkaufter Menge wird über eine Korrelation zwischen diesen beiden Variablen abgebildet. Der Vollständigkeit halber modellieren wir noch eine Dummy Variable, welche nicht in die Gewinnberechnung einfliesst (siehe Excel-Tabellenblatt «Eisdiele» für die Modellspezifikation mit den Variablen).
Folgend das Resultat nach 10'000 Iterationen, hier dargestellt am Gewinn:
So sehen wir, dass der Gewinn - angewandt auf unser in Zahlen gemünztes Vorwissen - zwischen ca. -3'933 CHF und ca. 5'497 CHF (siehe Minimum und Maximum) zu liegen kommen kann. Wir können nun unsere Ereignisse A und B analog oben definieren und die entsprechenden Berechnungen auslösen.
Die Menge der 10'000 Iterationen entspricht der Grundgesamtheit Ω. Weiters formulieren wir folgende Ereignisse:
A ist die Anzahl Ereignisse, bei denen der Gewinn mindestens 0 beträgt.
B ist die Anzahl Ereignisse, bei denen die Anzahl verkaufter Kugeln maximal 3’500 beträgt.
C ist die Anzahl Ereignisse, bei denen die Dummy Variable grösser 0 ist.
Unsere Ausgangsfrage ist: «Mit welcher Wahrscheinlichkeit wird der Gewinn mindestens 0 betragen, gegeben dass die Anzahl verkaufter Eiskugeln maximal 3'500 beträgt?»
Um zur Lösung zur kommen, müssen wir nach P(A|B) auflösen. Sowohl P(B), P(A) als auch P(B|A) sind aus der Simulation bekannt, respektive aus dieser ableitbar (siehe Zellen P8:P10), womit nach Anwendung der Bayes Formel (siehe Zelle U8) die Lösung ermittelt werden kann. In diesem Fall ist P(A|B) ca. 19%. Es geht natürlich auch einfacher (und genauer), wenn wir direkt die MC FLO Formel «=fmc_Bayes» in Zelle U9 anwenden.
Ohne Kenntnis weiterer Information lag unsere Auffassung über die Wahrscheinlichkeit, dass wir einen Gewinn erzielen werden, bei ca. 92% (P(A), Zelle P8). Durch die zusätzliche Informationen hinsichtlich der Absatzmenge von maximal 3'500 Eiskugeln, hat sich unser Wissen bezüglich der Gewinnprognose neu geformt und ist auf 19% gesunken. Die Menge steht somit in Zusammenhang mit dem Gewinn.
Anders sieht es hingegen bei der «Dummy» Variable aus. P(A|C) soll folgenden zusammengesetzten Ausdruck darstellen: «Mit welcher Wahrscheinlichkeit wird der Gewinn mindestens 0 betragen, gegeben dass die Dummy-Variable mindestens 0 beträgt?». Die Lösung aus Zelle U11 ist gleich der Lösung P(A). Da die «Dummy» Variable nicht in der Gewinnformel (weder direkt noch indirekt) vorkommt, besteht kein Zusammenhang zwischen A und C, womit das Ergebnis einleuchtet. Also ist P(A|C) = P(A).
Ein Wort zur Vorsicht (ohne zu sehr in die Kausalanalyse einzutauchen): Nur weil die Absatzmenge mit dem Gewinn in Zusammenhang steht, heisst dies nicht, das hier eine kausale Beziehung besteht. Offensichtlich ist es so, dass das gute Wetter für eine Erhöhung der Absatzmenge und somit zur ex-ante Prognose von 92% Gewinnwahrscheinlichkeit geführt hat.
Die Logik dahinter kann durch folgende Aussagen gestützt werden:
«Das Wetter ist schön, also werden die Leute mehr Eis essen, was zu einer Erhöhung der Gewinnprognose führt»
Wäre die Absatzmenge hingegen kausal, wären folgende Aussagen logisch konsistent:
«Die Leute gehen mehr Eis essen, also wird das Wetter schön, was zu einer Erhöhung der Gewinnprognose führt».
In unserer Gewinnformel kommt das Wetter nicht vor, aber da die Absatzmenge mit dem Wetter «korreliert», leuchtet es ein, dass die Ursache für die Gewinnverteilung durch das Wetter bestimmt wird. Folgend die modellierte Korrelation zwischen der (zukünftigen) Absatzmenge und der erwarteten Ausprägung des Wetters (welche über eine Beta Verteilung hergeleitet wurde).
Gehen wir nur langsam zu unserer Likelihood über…aber langsam.
Folgend haben wir alle Ergebnisse der Simulation als Tabellenform (oder auch bekannt als Vier-Felder-Matrix) in Zelle O22ff. abgetragen (beachten Sie, dass mit jeder Simulation die Ergebnisse leicht davon abweichen können).
Von den 10'000 Iterationen der Simulation fallen 757 Iterationen in die Kategorie «weniger oder gleich 3'500 Kugeln verkauft» und «Gewinn ist negativ». Unsere gesuchte Grösse P(A|B) kann ebenfalls aus dieser Tabelle abgetragen werden. So sehen wir, dass insgesamt 936 Iterationen das Ergebnis «Anzahl verkaufter Eiskugeln beträgt maximal 3’500» aufweisen, davon sind 179 Ergebnisse mit einem Gewinn grösser gleich Null verbunden. 179/936 ≈ 19%.
Um zu unserer Likelihood zu kommen gehen wir einen anderen Weg. Wir evaluieren für die verschiedene Gewinngrössen die Menge. Wir fragen uns Folgendes: Ist ein Gewinn grösser Null oder ein Gewinn kleiner Null mit der Mengenplanung kompatibel? Um den Begriff der Wahrscheinlichkeit zu umgehen (warum, sehen wir gleich), wird für die Likelihood das Kürzel «L» verwendet. L(A|B) steht somit für die Frage, ob das Ereignis A mit dem Ereignis B kompatibel ist. Um dies beantworten zu können, sind alle möglichen Ereignisse A, welche auftreten können zu evaluieren. Technisch ist in unserem Fall nach P(B|A) und P(B|Ac) aufzulösen, wobei «c» für Komplement steht und P(A) + P(Ac) = 1 ergibt.
P(B|A) entspricht der Wahrscheinlichkeit, dass die Absatzmenge <= 3'500 beträgt, gegeben dass der Gewinn höher oder gleich Null beträgt. Diese Wahrscheinlichkeit beträgt 2% (siehe Zelle P10). P(B|Ac) entspricht der Wahrscheinlichkeit, dass die Absatzmenge <= 3'500 beträgt, gegeben dass der Gewinn geringer als Null beträgt. Diese Wahrscheinlichkeit beträgt 100% (siehe Zelle U21).
Hier kommen wir zur einen prägenden Eigenschaft der Likelihood: Die Summe deren Wahrscheinlichkeiten ist nicht gleich 100%. In unserem Fall sind es 102%. Likelihoods sind somit keine klassischen Wahrscheinlichkeiten, deren Summe 1 oder 100% betragen muss. Dies ist der Grund, warum Likelihoods nicht mit einem «P» vorangestellt werden. Die zweite und entscheidende Eigenschaft: Likelihoods ergeben für sich alleine keinen Sinn, sondern sind immer in Bezug zu setzen. So sehen wir, dass ein Gewinn kleiner gleich 0 in Verbindung mit einer Absatzmenge bis max. 3'500 Eiskugeln eher möglich ist, als ein Gewinn grösser Null in Verbindung mit der gleichen Absatzmenge. Die Chancen hierzu stehen 50:1 (100% / 2%). Das heisst, das ein Gewinn kleiner Null eher mit tiefen als mit hohen Absatzmengen kompatibel ist. Der Relationscharakter der Likelihood wird uns gleich noch einmal begegnen.
Abstrahieren wir das Ganze ein wenig
A = Hypothese, etwa wonach mein Gewinn grösser 0 sein wird = H
B = Daten, etwa meine Absatzmengen = D
Ausserdem gilt zudem:
Das heisst, wir suchen nach der Schnittmenge zwischen Hypothese und den Daten, um unsere gesuchte Wahrscheinlichkeit zu bestimmen. Unschön an dieser Formel ist, dass nach P(D), also der Wahrscheinlichkeit, dass unsere Daten auftreten, aufgelöst wird.
Greifen wir unser Beispiel nochmals auf.
Unsere Kernfrage war: «Mit welcher Wahrscheinlichkeit wird der Gewinn mindestens 0 betragen, gegeben dass die Absatzmenge maximal 3'500 Eiskugeln beträgt?». Wir suchten somit nach P(A|B), wobei B für maximal 3'500 Eiskugeln stand. Das Ergebnis beträgt bekanntlich 19%.
Schauen wir uns den Zähler der obigen Bayes Formel an: P(B|A)*P(A).
P(B|A) entspricht unserer Likelihood L(A|B) und P(A) stellt unser Vorwissen über die Gewinnwahrscheinlichkeit >= 0 ohne weitere Informationen dar. Kern unser Überlegung ist somit die Likelihood (von Tarski/Popper kennen wir der Begriff der «Wahrheitsnähe», was unseres Erachtens den Sachverhalt besser trifft): welche Ausprägungen von A sind mit den gegebenen Daten B kompatibel? Eine andere, allgemeine Formulierung der Likelihood ist folgende: welche Hypothese nähert sich am besten den Daten an? Hierfür variieren wir unsere Hypothese und schauen uns an, ob die Daten mit den jeweiligen Hypothesen kompatibel sind.
Unsere Ursprungshypothese P(H) oder P(A) war, dass der Gewinn mindestens oder grösser Null ist. Die Alternativhypothese lautet daher, dass der Gewinn negativ ist.
Für beide Konstellationen haben wir die entsprechenden Wahrscheinlichkeiten abgetragen (die Details können dem Excel entnommen werden):
Wie bereits mehrmals erwähnt, beträgt die Wahrscheinlichkeit einen Gewinn gleich oder grösser Null zu erzielen, gegeben dass die Menge verkaufter Eiskugeln maximal 3'500 beträgt, 19%. Umgekehrt bedeutet es, dass die Wahrscheinlichkeit einen Gewinn kleiner Null zu erzielen, gegeben dass die Menge verkaufter Eiskugeln maximal 3'500 beträgt, 81% (100%-19%) betragen muss. Das Verhältnis dieser beiden Grössen beträgt 4.2 (81%/19%).
In der Zeile 33 haben wir die Likelihood (L) für beide Gewinnhypothesen dargestellt. So ist ersichtlich, dass ein Gewinn grösser gleich Null, gegeben dass die Anzahl verkaufter Eiskugeln höchstens 3'500 Einheiten beträgt, mit 2% weniger plausibel erscheint als die Kombination eines Gewinnes kleiner Null mit der Anzahl von höchstens 3'500 Eiskugeln (100%).
Oder: L(Gewinn kleiner Null |Anzahl verkaufter Eiskugeln maximal 3'500) > L(Gewinn gleich oder grösser Null |Anzahl verkaufter Eiskugeln maximal 3'500).
Zur Vervollständigung des Zählers gemäss obiger Formel müssen wir jeweils die Likelihood mit der Ursprungswahrscheinlichkeit P(Gewinn) multiplizieren, was in der Zeile 32 vorgenommen wurde. Die Kombination L*P(A), wobei A einmal für das Ereignis Gewinn grösser gleich Null (Spalte 1) und einmal für Ereignis Gewinn kleiner Null (Spalte 2) steht, resultiert in Werte von 1.79% und 7.57%. Das Verhältnis der Zählers (Ratio) beträgt ~4.2. Wie aus oben ersichtlich, haben wir dieses Verhältnis durch den Beizug der vollständigen Bayes Formel – unter Einschluss des Nenners - ebenfalls berechnet. Wenn wir uns nur noch auf Verhältnisse beschränken, was bei einem Vergleich unterschiedlicher Hypothesen nicht abwegig ist, können wir auf eine Division des «Normierungsfaktors» P(B) oder allgemein P(D) verzichten! Aus diesem Grund: Likelihoods sind als Verhältnisgrösse zu anderen Likelihoods zu sehen.
Wow. Wir können unsere Berechnungen vereinfachen und somit uns auf das Produkt aus L(H|D)*P(H) zur Lösung von P(H|D) beschränken. Wir wissen zwar, dass die Summe aller möglichen L(Hi|D), wobei i für 1…n steht, nicht 1 betragen wird, aber die relativen Ergebnisse, etwa L(H1|D)*P(H1) zu L(H2|D)*P(H2) verhalten sich proportional zum echten Ergebnis.
Anstatt die Bayes Formel unter Einschluss von P(D) zu berechnen, beschränkt man sich in der Praxis daher auf das Lösen von L(H|D) * P(H); oder auch P(H|D) ∝ L(H|D) * P(H), was wie folgt interpretiert werden kann: «Die Wahrscheinlichkeit, dass unsere Hypothese bei gegebenen Daten zutrifft, ist proportional zur Likelihood multipliziert mit der Ursprungswahrscheinlichkeit der Hypothese».
Eine allgemeinere Formulierung für P(H|D) ∝ L(H|D) * P(H) ist Folgende:
«A-Posteriori» Wissen ∝ Likelihood * «A-priori» Wissen
Sprich: Unser Wissen über die Hypothese, nachdem wir die Daten beobachtet haben (neues, angepasstes Wissen oder auch «A-Posteriori» Wissen), ist proportional zur Likelihood multipliziert mit dem Vorwissen (oder auch «A-Priori» Wissen).
Das Ganze für verschiedene Hypothesen zu erstellen, wird per Hand dann doch etwas mühsam. Zum Glück können wir Dank moderner Rechner und unter Rückgriff auf mächtige Algorithmen, wie den Metropolis-Hastings Algorithmus, das «A-Posteriori» Wissen relativ einfach formen. Womit wir das nächste Kapitel aufschlagen....
*Die frequentistische Auffassung der Statistik wendet hier den Begriff der Wahrscheinlichkeit nicht an. Entweder eine Person spielt in einem Berufsorchester oder nicht.

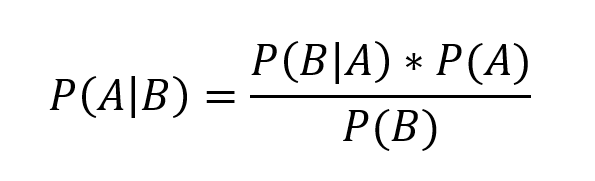









Kommentar schreiben